绝美的超级实用的数学模型——杨辉三角
如果需要用一个东西来代表数学,我想杨辉三角是再合适不过的了
且听我徐徐道来:
- 杨辉三角&维度
- 杨辉三角&代数
- 杨辉三角&组合
- 杨辉三角&概率
- 杨辉三角&斐波那契
What is杨辉三角
直接看一个就知道了嘛:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
是不是很熟悉?规律也很明显?
不过,这并不是杨辉三角的全貌,原版应该是这样的
0 1 0
0 1 1 0
0 1 2 1 0
0 1 3 3 1 0
0 1 4 6 4 1 0
0 1 5 10 10 5 1 0
按照递推定义:杨辉三角的每一个数字应该是他左上和右上的两数字和
实际上,我们也经常用到这样的写法
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
这种写法是程序里面见得比较多的,按照这种写法我们可以使用一下递推式子实现生成杨辉三角
memset(a,0,sizeof(a));a[0][1]=1;//初始化
//递推式
a[i][j]=a[i-1][j]+a[i-1][j-1];
看起来,杨辉三角单纯,简单,仅仅使用加法就可以得到
但是,杨辉三角并不单纯,它蕴藏着无数的秘密和玄机
杨辉三角&维度
先拿出我们的杨辉三角一个!
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
然后呢?抽一条出来
怎么抽,就先抽三角形的最外层的那个边吧
1 1 1 1 1 1 1 1 1………………
就是这个啦!
看起来平平无奇?
这个其实叫常数序列啦!也就是序列没有任何的变化,整个序列都是一个数字
别小看它,它的另一种叫法叫做 零维序列
零维,也就是奇点,这是宇宙的开始,也是杨辉三角的开始,从0,到1
紧紧挨着的,这一条,叫做一维序列,这样的
1 2 3 4 5 …………
一定要对照三角找一下这一条在哪里哦!
这一条,是一个单调递增1的线性序列,它又叫做一维序列
而下一个,就是大家耳熟能详的三角序列了!
紧紧挨着1维序列的那个!
1 3 6 10 …………
这个,规律貌似并不好找,但是我们画出图来理解试试?
*
1
*
* *
3
*
* *
* * *
6
*
* *
* * *
* * * *
10
现在是否好理解了?
就是堆成三角形的个数呀!
但是,看上去好像明白了,实际上却并不明白!
因为,三角形序列远远不止这么简单!
我们给三角序列求差,看好!
1 3 6 10 ……………
+2 +3 +4 …………
因为,这其实就是一维序列的前缀和呀!
这是一维序列!
1 2 3 4 5 6 7 8………………
求它的前缀和!
1 3 6 10 15 21…………
所以!能否理解!一个一个一维的线,堆积堆积起来,其实就是二维!
而这个三角形序列,又叫平面三角序列,或者叫二维三角序列!
实际上,我们就可以叫他二维序列!
反过头来看上一个一维序列和零维序列,其实是不是也是这个关系呢?
一维序列就是零维序列的前缀和啊!
一个一个点,堆成线,一个一个线,堆成面
那么接下来呢?
我们看接下来一行!长这样:
1 4 10 20 35 ………………
按照我们之前的规律,这个应该是?
三位序列!实际上更加广为人知的名字是:立体三角序列
不信你自己在脑子里摆一个三角堆(四面体)看看
所需要的小球数量按总层数来就是这个序列!
除此之外,意料之中的是,它也是二维序列的前缀和序列!
那么,按照这个规律下去,4维序列,5维序列,甚至n维序列,我们都可以得到
而这一切,其实都是起源于一个零维序列……
于是按照这个思路,我们又可以依照前缀和的思路生成杨辉三角形啦!
而且,按照这个前缀和思路,你会发现一个小特点:
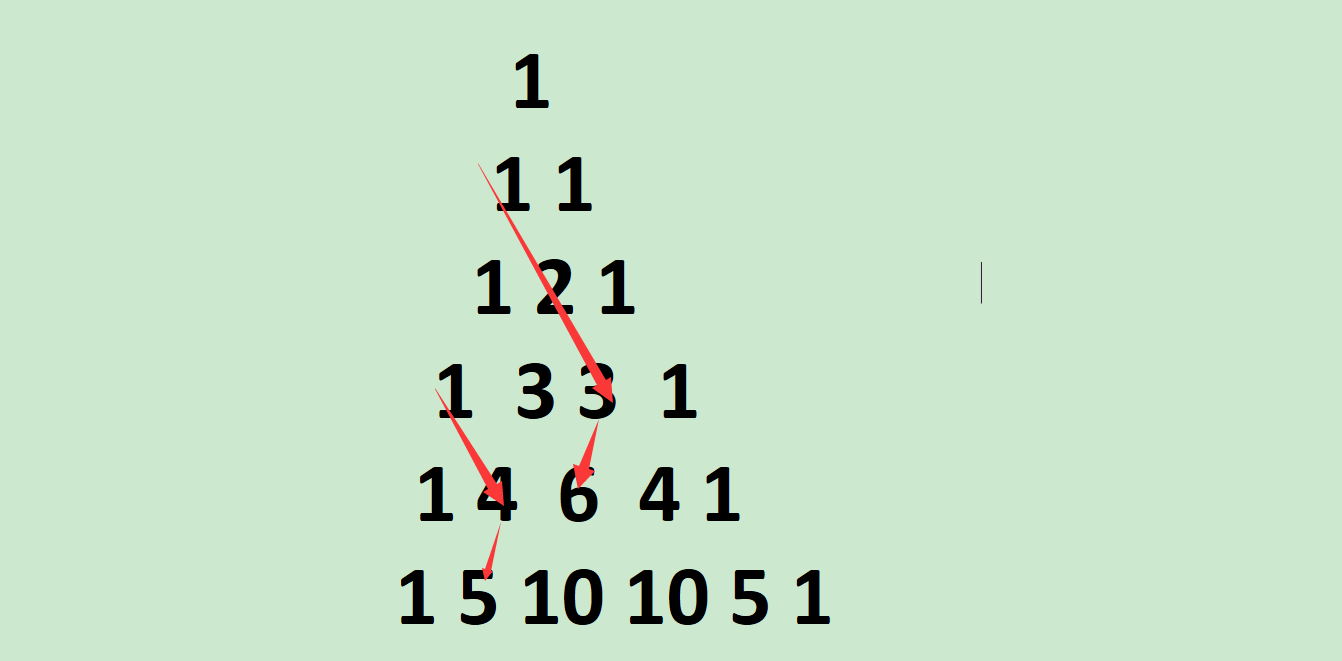
当你沿着某一条序列走的时候,突然拐角,就会的到你之前走过的所有数字的和!
当然,我们现在看到的,仅仅是杨辉三角的冰山一角!
杨辉三角&代数
拿出三角形,别忘了!
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
我们试着把每一个数字都写出来?
1
11
121
1331
14641
发现了吗?
这不就是:11^0,11^1,11^2,11^3,11^4吗?
但是你又说,第五个呢?
如果我们把10进位,就会得到161051,就是11^5
但是,我们还有更NB的!
首先是大家耳熟能详的二项式定理
?什么是二项式定理?
那完全平方公式你总知道吧
(a+b)^2= a^2 + b^2 + 2ab
如果我们按a的降幂排列,就是这样:a^2 + 2ab + b^2
由此,我们也可以想到:完全一次方公式,完全三次方公式…………
写一下!
(a+b)^1=a + b
(a+b)^2=a^2 + 2ab + b^2
(a+b)^3=a^3 + 3a^2b + 3ab^2 + b^3
…………
诶?你没发现吗?
我们把系数写下来!
1 1
1 2 1
1 3 3 1
这!就是杨辉三角!
而杨辉三角,可以非常高效的回答二项式定理的系数问题!
而根据二项式定理,我们又可以推出:第i层杨辉三角的数的和为2^i
看吧
1 0层 2^0=1
1 1 1层 2^1=2
1 2 1 2层 2^2=4
1 3 3 1 3层 2^3=8
………………
至于证明,其实就是二项式定理,设a=1,b=1
(1+1)^n,就是系数和!
这么,我们就完美的得到了二项式定理生成杨辉三角的方案和杨辉三角完成二项式定理的打表方案!
杨辉三角&组合
你一定见过这类问题:
某城市的街道是一个很规整的矩形网络,有3条南北向的纵街,4条东西向的横街。现要从西南角的A走到东北角的B,最短的走法共有多少种?
这个时候,你就会老老实实算C(2,5)
但是,当这个东东放到杨辉三角里就不一样了!
上三角!
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
上图!
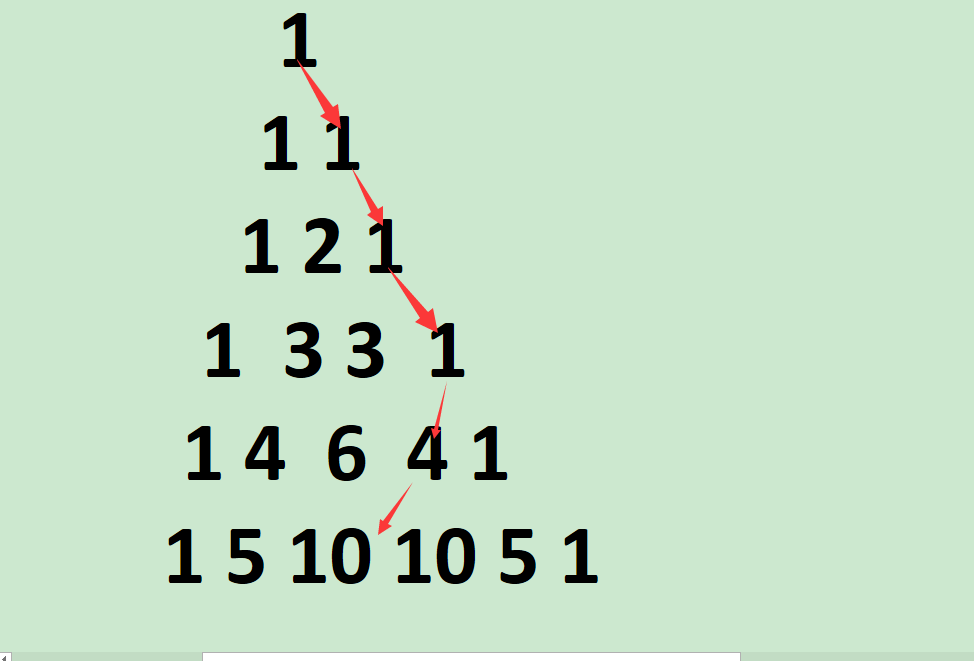
其实问题转化一下很好理解,就是走两次左侧,走三次右侧!
走到的是..10?
跟答案一模一样?
这不是巧合,而是因为,所有的组合数,都藏在了杨辉三角里!
我们用下面的这个三角讲:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
看好!下面的将会是一一对应的!
c(0,0)
C(0,1) C(1,1)
C(0,2) C(1,2) C(2,2)
C(0,3) C(1,3) C(2,3) C(3,3)
C(0,4) C(1,4) C(2,4) C(3,4) C(4,4)
C(0,5) C(1,5) C(2,5) C(3,5) C(4,5) C(5,5)
翻译翻译,什么叫NB!
完全一一对应!
看上去确实和九九乘法表有点像hh
而我们同时也就知道了,从杨辉三角的顶点到三角中任意一点的最短路径数量,就是他自己!
这样子,我们就有了一个棒极了的组合数生成杨辉三角方案和杨辉三角打表组合数方案!
P.S.还有两个以后再更,太懒了hh
总结
杨辉三角对OI有什么意义,对开发又有什么意义?
我觉得已经不言而喻
只要提前准备好了杨辉三角,就相当于同时完成了所有包括组合数,二项式系数,和N维序列的O(1)查询!
杨辉三角的奥妙,远远不止于此,这是来自一千年前的光,照回了起源,照出了未来
Over~


666
Oz