历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AtCoder Beginner Contest 216 个人题解

作者：

小飞龙 , 2021-08-30 20:01:53 , 所有人可见 , 阅读 646

3

1

AtCoder Beginner Contest 216 个人题解

比赛链接：AtCoder Beginner Contest 216

每篇一图

QQ截图20210824214654.png

A题 Signed Difficulty

题目大意：

给出一个小数，根据小数部分改写 $+，-$

思路解析：

直接判断即可

AC代码：

#include<bits/stdc++.h>
using namespace std;
int main(){
    int x,y;
    scanf("%d.%d",&x,&y);
    if(y<=2)cout<<x<<"-"<<endl;
    else if(y<=6)cout<<x<<endl;
    else cout<<x<<"+"<<endl;
}

B题 Same Name

题目大意：

给出 $n$ 个人的名字，每个人的名字由两部分组成，问是否有重名的人

思路解析：

暴力枚举匹配
STL-map判断

AC代码：

暴力做法

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+5;
struct node{
    string x,y;
}s[maxn];
int main(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>s[i].x>>s[i].y;
    int flg=0;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(i==j)continue;
            if(s[i].x==s[j].x&&s[i].y==s[j].y)flg=1;
        }
    }
    if(flg)cout<<"Yes"<<endl;
    else cout<<"No"<<endl;
}

map做法

#include<bits/stdc++.h>
using namespace std;
map<string,map<string,int> >a;
string s,t;
int n;
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>s>>t;
        if(a[s][t]){
            cout<<"Yes"<<endl;
            return 0;
        }
        a[s][t]=1;
    }
    cout<<"No"<<endl;
}

C题 Many Balls

题目大意：

有一个盒子，你可以进行两种操作：1.往盒子里放一个球 2.使盒子里的球翻倍
问一个可行的操作方案使盒子里的球从 $0$ 到 $n$ ，操作最多 $120$ 次

思路解析：

我们很容易想到可以从 $n$ 往回推，这样操作 $1$ 就变成了 $/2$ ，操作 $2$ 就变成了 $-1$ ，当$n$ 为偶数，就可以 $/2$ 当，$n$ 为奇数就可以 $-1$ ，直到盒子里的球为 $0$

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(){
    ll n;
    cin>>n;
    string ans;
    while(n){
        if(n%2==0){
            ans+='B';
            n/=2;
        }
        else{
            ans+='A';
            n--;
        }
    }
    for(int i=ans.size()-1;i>=0;i--)cout<<ans[i];
}

D题 Pair of Balls

题目大意：

我们有 $n$ 种颜色的球，每种颜色有两个球，总共有 $2n$ 个球，这些球被放在 $m$ 个栈中，每次只能从两个不同栈顶取出相同颜色的球，问是否可以把球全部取出~~（好像消消乐）~~

思路解析：

首先我们思考，很直观的考虑，什么时候会不能达成目的：
灵魂画手上线：

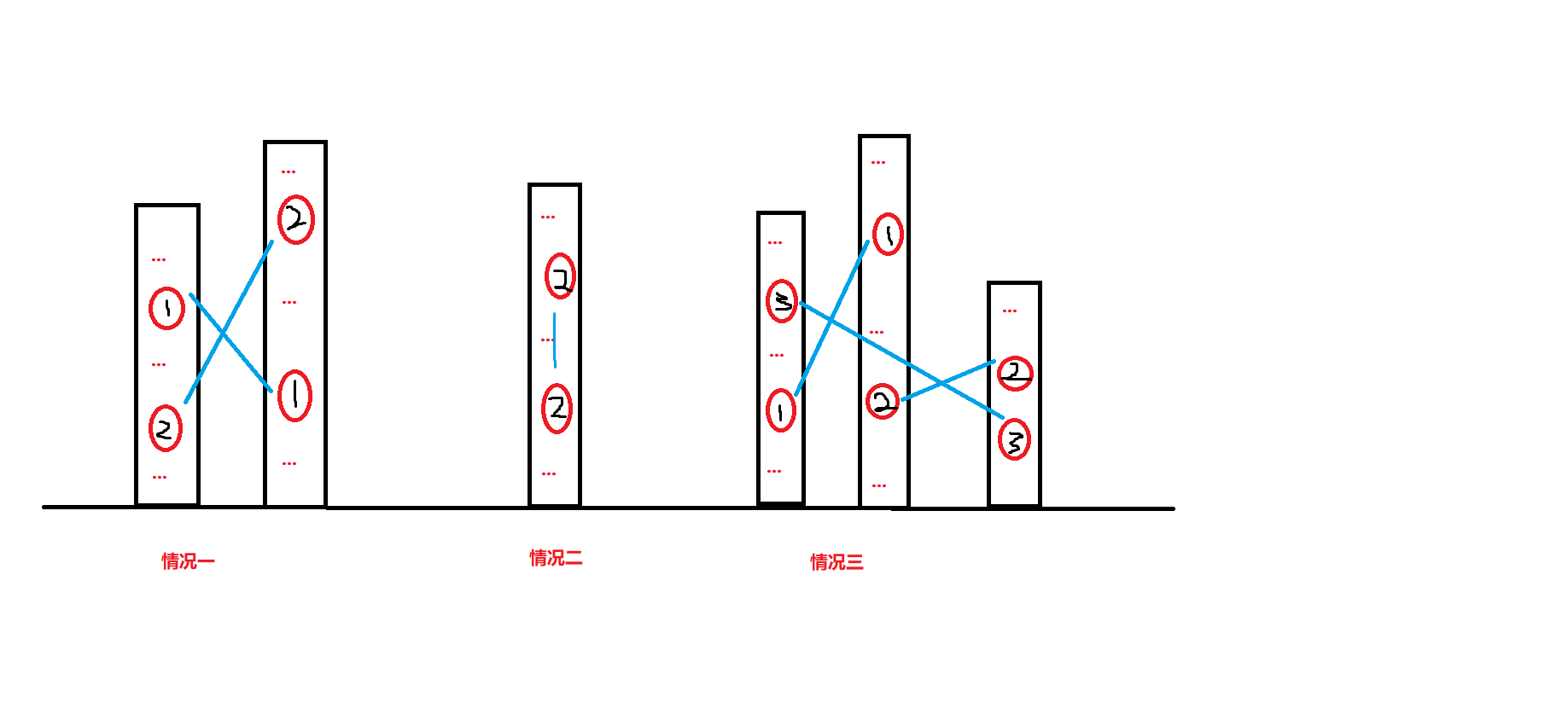
无标题.png

由题意我们很容易看出，如果要想清空一个栈的话每个栈顶的数字一定需要先于他下面的数删除，所以这就形成了拓扑关系。
在观察数据，我们又可以发现由于每个数字存在两个，所以以每个数字为节点，至多向外连两条有向边，我们就可以把问题转化为了有向图的拓扑排序来处理。

解压密码：[HTML_REMOVED]数据加强，以上为假思路！[HTML_REMOVED]

修正：

开栈模拟

假思路代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=4e5+5;
int e[maxn],h[maxn],nex[maxn],id;
int ans,in[maxn];
queue<int>q;
void add(int x,int y){
    e[++id]=y;
    nex[id]=h[x];
    h[x]=id;
}
int main(){
    int n,m;
    cin>>n>>m;
    for(int j=1;j<=m;j++){
        int k,pre,x;
        cin>>k>>pre;
        for(int i=2;i<=k;i++){
            cin>>x;
            add(x,pre);
            in[pre]++;
        }
    }
    for(int i=1;i<=n;i++){
        if(in[i]==0)q.push(i);
    }

    while(q.size()){
        int top=q.front();
        q.pop();
        ans++;
        for(int i=h[top];i;i=nex[i]){
            int j=e[i];
            in[j]--;
            if(in[j]==0)q.push(j);
        }
    }
    if(ans==n)cout<<"Yes"<<endl;
    else cout<<"No"<<endl;
}

AC代码

#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
typedef long long ll;
const int maxn=8e5+5;
int pos[maxn][3];
stack<int>s[maxn];
queue<pii>q;
int sum[maxn];
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int k,op;
        cin>>k;
        for(int j=1;j<=k;j++){
            cin>>op;
            s[i].push(op);
            if(pos[op][0]==0)pos[op][0]=i;
            else pos[op][1]=i;
        }
        sum[s[i].top()]++;
        if(sum[s[i].top()]==2)q.push(make_pair(pos[s[i].top()][0],pos[s[i].top()][1]));
    }
    while(!q.empty()){
        pii top=q.front();
        q.pop();
        s[top.first].pop();
        if(s[top.first].size())
        {
            sum[s[top.first].top()]++;
            if(sum[s[top.first].top()]==2)
            q.push(make_pair(pos[s[top.first].top()][0],pos[s[top.first].top()][1]));
        }
        s[top.second].pop();
        if(s[top.second].size())
        {
            sum[s[top.second].top()]++;
            if(sum[s[top.second].top()]==2)
            q.push(make_pair(pos[s[top.second].top()][0],pos[s[top.second].top()][1]));
        }
    }
    for(int i=1;i<=m;i++){
        if(s[i].size()){
            cout<<"No"<<endl;
            return 0;
        }
    }
    cout<<"Yes"<<endl;
}

E题 Amusement Park

题目大意：

给你 $n$ 个数，你可以选择 $k$ 次，每次选择一个数后这个数就会 $-1$ ，问你能得到选择数的和的最大值

思路解析：

首先我们考虑暴力的做法：直接把数都扔到 set 里，每次取最大然后让他 $-1$ 再把它扔回去就行了，但是这么做稳 $TLE$
如何优化：推一推，手搓一下就完了

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+5;
ll n,k,a[maxn],cnt,ans;
bool cmp(ll x,ll y){
    return x>y;
}
int main(){
    cin>>n>>k;
    for(int i=1;i<=n;i++)cin>>a[i];
    sort(a+1,a+n+1,cmp);
    for(int i=1;i<=n;i++){
        ll x=a[i]-a[i+1];
        if(cnt+i*x<=k){
            ans+=(a[i]+a[i+1]+1)*x/2*i;
            cnt+=i*x;
        }
        else{
            k-=cnt;
            ans+=(a[i]+a[i]-(k/i)+1)*(k/i)/2*i;
            ans+=(k%i)*(a[i]-(k/i));
            break;
        }
    }
    cout<<ans<<endl;
}