显然“从前有座山……”这个故事描述的是递归算法。和尚讲的故事里继续套用和尚讲故事，，正如函数不断调用本身，形成递归。

“(A \lor B) \land \lnot A(A∨B)∧¬A”选项，当 AA 为真的时候，此式恒为假，当 A假的时候，值取决于 B

“(A \lor B) \land \lnot B(A∨B)∧¬B”选项，当 BB 为真的时候，此式恒为假，当 B为假的时候，值取决于 A

“(A \land B) \lor ( \lnot A \land B)(A∧B)∨(¬A∧B)”选项，当 B真的时候，此此式恒为真，当 B 为假的时候，此式子恒为假，结果与 AA 的真假无关。

“(A \lor B) \land \lnot A \land B(A∨B)∧¬A∧B”选项，当 BB 为真的时候，此式结果为 \lnot A¬A，于 AA 有关，当 BB 为假的时候，此式恒为假。

对于任意一颗二叉树，度为0的节点数等于度为2的节点数加一。所以在一颗含10个结点的二叉树中，度为2的节点数最多为4，如果超过4，则总节点数将超过10. A


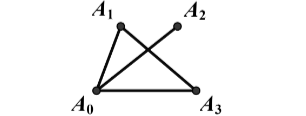
从途中可以知道，从A0开始可能性：
A0,A1,A3,A2
A0,A3,A1,A2
A0,A2,A1,A3
所以选项A不可以，因为这个路径从一个点开始只能一直走到头不能改变。 A

IPv4 协议使用 3232 位地址，IPv6 协议则使用 128128 位地址，可以有效地解决地址资源枯竭的问题。D

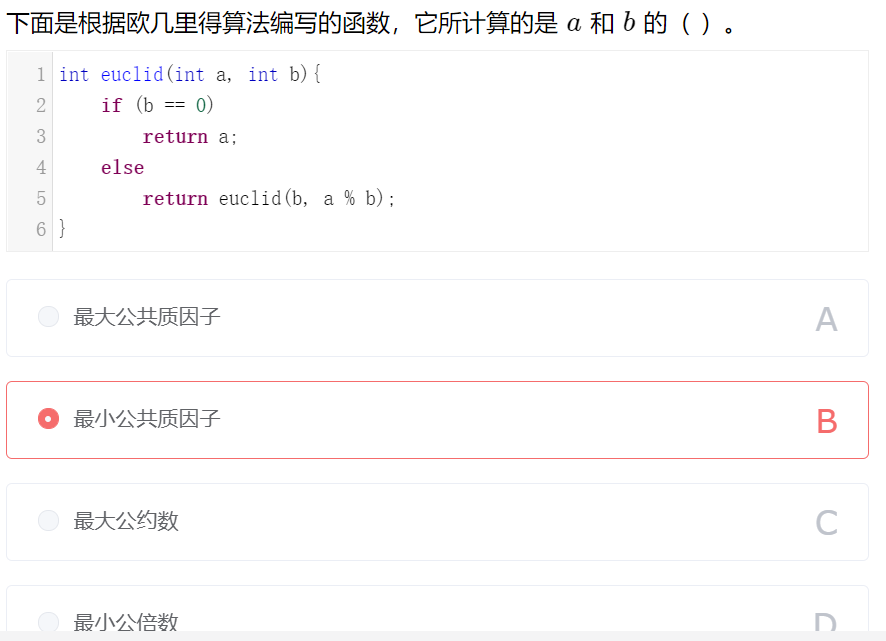
欧几里得算法是用来计算a和b的最大公约数。C

题目解析

由题意可以列出以下方程组：

(s_1+s_2)\bmod 2=1(s 
1
​   
 +s 
2
​   
 )mod2=1

(s_3+s_4)\bmod 2= 0(s 
3
​   
 +s 
4
​   
 )mod2=0

(s_2+s_3)\bmod 2=0(s 
2
​   
 +s 
3
​   
 )mod2=0

(s_1+s_2+s_3)\bmod 2=0(s 
1
​   
 +s 
2
​   
 +s 
3
​   
 )mod2=0

(s_1)\bmod 2=0(s 
1
​   
 )mod2=0

解得 s_1 = 0, s_2 = 1, s_3 = 1, s_4 = 1s 
1
​   
 =0,s 
2
​   
 =1,s 
3
​   
 =1,s 
4
​   
 =1。由此可见，这个系统并不安全，多次问答的过程会导致密码泄露。事实上，只要该系统要求用户以 pp（0<p<\dfrac120<p< 
2
1
​   
 ）的概率故意答错，就能有效地避免窃听。可以证明，此时即使所有通信被泄露，破解密码也是非常难的。

#include <iostream>
using namespace std;
const int SIZE = 100;
const int INFINITE = 1000000;
struct node {
    int left_child, right_child, value;
};
node a[SIZE];
int is_bst(int root, int lower_bound, int upper_bound){
    int cur;
    if (root == 0)return 1;
    cur = a[root].value;
    if ((cur > lower_bound) && ( ① ) &&
    (is_bst(a[root].left_child, lower_bound, cur) == 1) && (is_bst(②,③,④) == 1))
        return 1;
    return 0;
}
int main(){
    int i, n;
    cin>>n;
    for (i = 1; i <= n; i++)
        cin>>a[i].value>>a[i].left_child>>a[i].right_child;
    cout<<is_bst( ⑤ , -INFINITE, INFINITE)<<endl;
    return 0;
}

题目答案

填空位置 ①：

cur < upper_bound

填空位置 ②：

a[root].right_child

填空位置 ③：

cur

填空位置 ④：

upper_bound

填空位置 ⑤：

1

题目要求检查输入的二叉树是否为二叉查找树，试题中使用了一个较为巧妙的函数is_bst来判断：

a)当前子树是否为二叉查找树

b)当前子树所有的值是否在区间 [lower_bound, upper_bound][lower_bound,upper_bound]内。

初始时，我们从根节点出发，并将 lower_boundlower_bound，upper_boundupper_bound 分别设为无穷小、无穷大。我们去检验当前该点值是否符合传递下来的范围，也就是是否在区间 [lower_bound, upper_bound][lower_bound,upper_bound]内。然后，检验左子树是否是二叉查找树，右子树是否是二叉查找树，如果 22 个子树都是二叉查找树，同时当前点的值也在范围内，说明以当前点为根的树也是二叉查找树。

剩下的问题就是如何检验子树是否是二叉查找树，这个问题利用递归就可以来解决，直接调用is_bst，同时传递子树以及更新边界的值，即[lower_bound, upper_bound][lower_bound,upper_bound]，如果是左子树则将 upper_boundupper_bound 修改为 curcur，如果是右子树则将 lower_boundlower_bound 修改为 curcur。直到发现root == 0也就是当前点为空，证明递归到终点。