题目答案
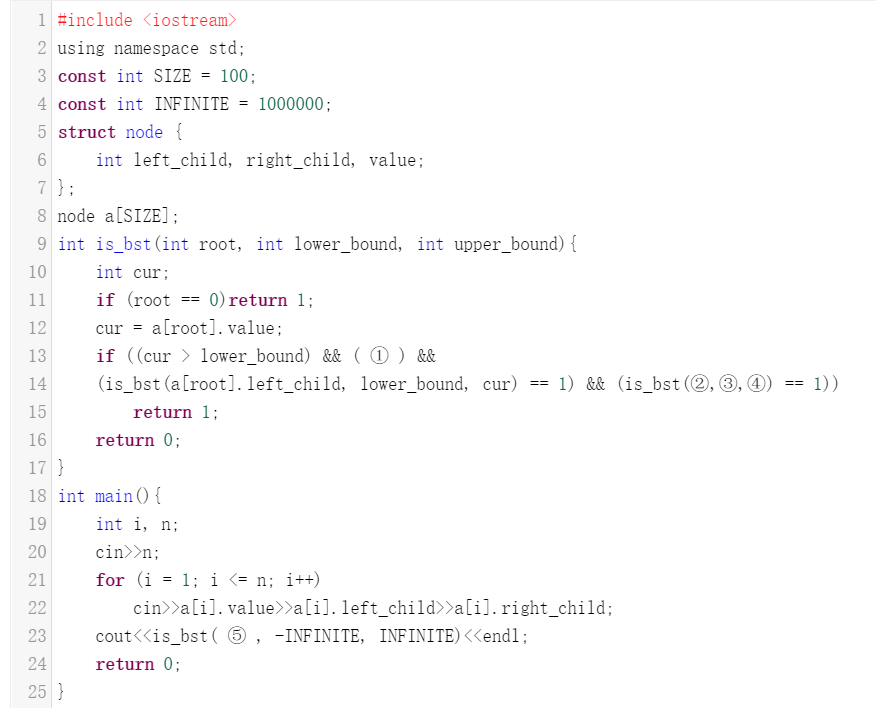
填空位置 ①：
cur < upper_bound
填空位置 ②：
a[root].right_child
填空位置 ③：
cur
填空位置 ④：
upper_bound
填空位置 ⑤：
1
题目解析
题目要求检查输入的二叉树是否为二叉查找树，试题中使用了一个较为巧妙的函数is_bst来判断：
a)当前子树是否为二叉查找树
b)当前子树所有的值是否在区间 [lower_bound, upper_bound][lower_bound,upper_bound]内。

初始时，我们从根节点出发，并将 lower_boundlower_bound，upper_boundupper_bound 分别设为无穷小、无穷大。我们去检验当前该点值是否符合传递下来的范围，也就是是否在区间 [lower_bound, upper_bound][lower_bound,upper_bound]内。然后，检验左子树是否是二叉查找树，右子树是否是二叉查找树，如果 22 个子树都是二叉查找树，同时当前点的值也在范围内，说明以当前点为根的树也是二叉查找树。

剩下的问题就是如何检验子树是否是二叉查找树，这个问题利用递归就可以来解决，直接调用is_bst，同时传递子树以及更新边界的值，即[lower_bound, upper_bound][lower_bound,upper_bound]，如果是左子树则将 upper_boundupper_bound 修改为 curcur，如果是右子树则将 lower_boundlower_bound 修改为 curcur。直到发现root == 0也就是当前点为空，证明递归到终点。

题目答案
填空位置 ①：
n - p + i
填空位置 ②：
a[i]
填空位置 ③：
n
填空位置 ④：
i - p + 1
填空位置 ⑤：
a[i - p]
题目解析
本题一共给出了 22 种算法：

第一种是开一个临时数组，将后 n - pn−p 个数和前 pp 个数依次拷贝到临时数组中，再把临时数组复制给当前数组。这一朴素的算法时间和空间复杂度均为 \mathcal{O}(n)O(n)。

第二种是每次把整个数组往左移一位(最左边的移到最后)，这样左移 pp 次即是最终的数组。省去了 \mathcal{O}(n)O(n) 的临时空间，但是时间复杂度上升至 \mathcal{O}(n2)O(n2)。

事实上还存在第三种算法，在时间和空间上结合了前两个算法的优点，具体做法是：取 pp 和 n - pn−p 之间的较小值，设为 qq，对调前 qq 个和后 qq 个元素，然后递归处理剩下长度为 n -2qn−2q 的子序列。具体代码实现读者可以参看提高组试题和解答。