题目答案

A

题目解析

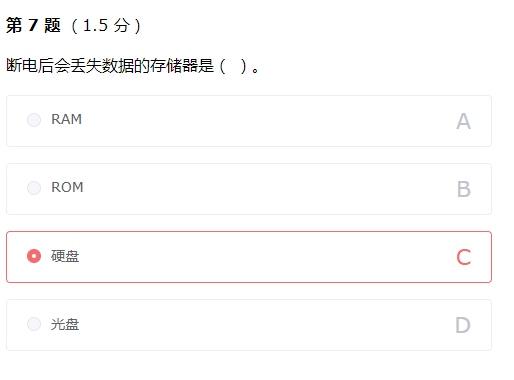
RAM 是随机存储器（Random Access Memory）的简称，存储单元的内容可按需随意取出或存入，是存取的速度与存储单元的位置无关的存储器，停电不保存信息。ROM 是只读存储器，数据的保存与是否通电无关。硬盘和光盘都是常见的数据载体，和是否通电无关。

题目答案

B

题目解析

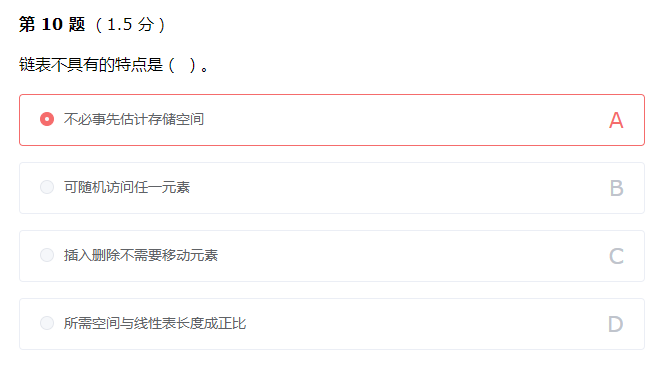
链表无法随机访问任意元素，查找任一节点都需要进行复杂度为 \mathcal{O}(n)O(n) 的顺序查找过程。链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域。相比于线性表顺序结构，操作复杂。由于不必须按顺序存储，链表在插入的时候可以达到 \mathcal{O}(1)O(1) 的复杂度，比另一种线性表顺序表快得多，但是查找一个节点或者访问特定编号的节点则需要 \mathcal{O}(n)O(n) 的时间。

题目答案

D

题目解析

无符号八位二进制数的表示范围为 00~2^8-12
8
−1，即 00 ~ 255255，因此选项 296296 与选项 256256 均不能表示。


题目答案

C

题目解析

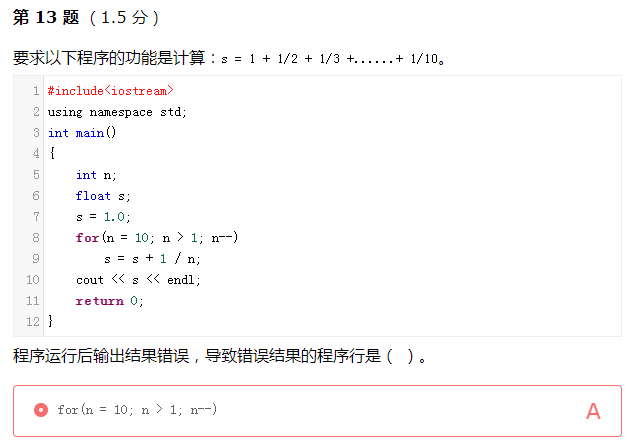
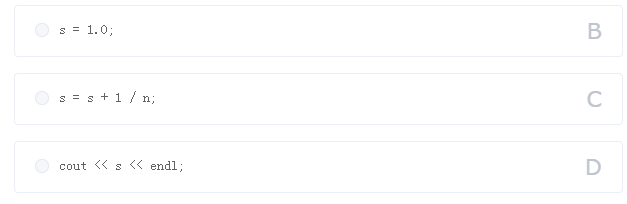
由于 nn 是整数，因此表达式中的 1 / n 会处理为整数除法，而这里我们需要的结果应该为实数。要使结果正确，需要使用实数除法，可以改为 1.0 / n或1 / (float)n等。

题目答案

A

题目解析

nn 层的满二叉树中节点数为 2^n-12
n
−1。

题目答案

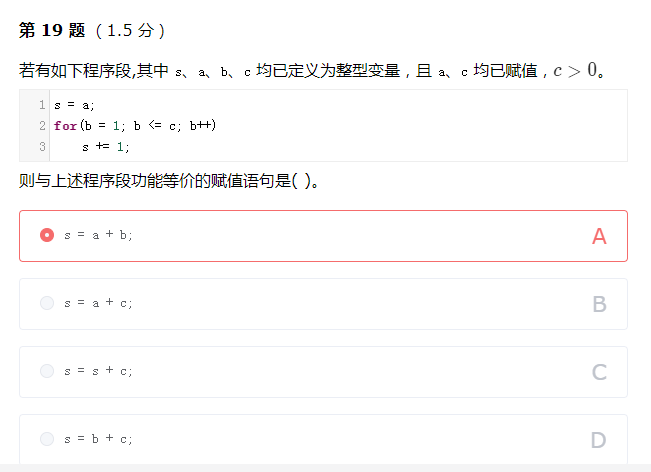
B

题目解析

s初值是a，循环体执行c次，每次加 11，因此 s = a + c。

include [HTML_REMOVED]

using namespace std;
int main()
{
int a, b, c, d, ans;
cin >> a >> b >> c;
d = a - b;
a = d + c;
ans = a * b;
cout << “Ans = ” << ans << endl;
return 0;
}
2 3 4
题目答案

Ans = 9

题目解析

按照顺序计算即可，注意不要漏掉提示信息“Ans = ”。

d=a-b=2-3=-1d=a−b=2−3=−1

a=d+c=(-1)+4=3a=d+c=(−1)+4=3

ans=a\times b=3\times =9ans=a×b=3×=9

因此正确答案为“Ans = 9”（不含引号，注意不要漏掉提示信息，也不要漏掉空格）。

include [HTML_REMOVED]

using namespace std;
int fun(int n)
{
if(n == 1)
return 1;
if(n == 2)
return 2;
return fun(n - 2) - fun(n - 1);
}
int main()
{
int n;
cin >> n;
cout << fun(n) << endl;
return 0;
}
7
题目答案

-11

题目解析

fun为递归函数，直接模拟难度较大。如果把fun视为数列，参数 nn 视为该序列的项数，则容易发现，该序列满足 fun(1) = 1, fun(2) = 2, n \ge 3fun(1)=1,fun(2)=2,n≥3时，fun(n) = fun(n - 2) - fun(n - 1)fun(n)=fun(n−2)−fun(n−1)。而本题的目标转化为求数列的第 77 项，因此可以使用递推依次计算数列各项：

include [HTML_REMOVED]

include [HTML_REMOVED]

using namespace std;
int main()
{
string st;
int i, len;
getline(cin, st);
len = st.size();
for(i = 0; i < len; i++)
if(st[i] >= ‘a’ && st[i] <= ‘z’)
st[i] = st[i] - ‘a’ + ‘A’;
cout << st << endl;
return 0;
}
Hello, my name is Lostmonkey.
题目答案

HELLO, MYNAMEISLOSTMONKEY.

题目解析

本题可以采用分析程序功能的方法，此程序的功能是：读入一个字符串，将字符串里的所有小写字母转化为相应的大写字母后输出。注意细心不要写错字母，漏掉标点符号以及空格。

include [HTML_REMOVED]

using namespace std;
const int SIZE = 100;
int main()
{
int p[SIZE];
int n, tot, i, cn;
tot = 0;
cin >> n;
for(i = 1; i <= n; i)
p[i] = 1;
for(i = 2; i <= n; i)
{
if(p[i] == 1)
tot++;
cn = i * 2;
while(cn <= n)
{
p[cn] = 0;
cn += i;
}
}
cout << tot << endl;
return 0;
}
题目答案

10

题目解析

此题可以通过直接模拟完成，不过细节比较多容易出错。经过简单的分析或模拟前几步就可以发现，此程序的功能就是用筛法求 nn 以内的质数，输出质数个数。而 3030 以内的质数有 2, 3, 4, 5, 11, 13, 17, 19, 23, 292,3,4,5,11,13,17,19,23,29 共 1010 个。
（数字删除）下面程序的功能是将字符串中的数字字符删除后输出。请填空。

1

include [HTML_REMOVED]

2
using namespace std;
3
int delnum(char *s)
4
{
5
int i, j;
6
j = 0;
7
for(i = 0; s[i] != ‘\0’; i)
8
if(s[i] < ‘0’ ① s[i] > ‘9’)
9
{
10
s[j] = s[i];
11
②;
12
}
13
return ③;
14
}
15
const int SIZE = 30;
16
int main()
17
{
18
char s[SIZE];
19
int len, i;
20
cin.getline(s, sizeof(s));
21
len = delnum(s);
22
for(i = 0; i < len; i)
23
cout << ④;
24
cout << endl;
25
return 0;
26
}
题目答案

填空位置 ①：

||

填空位置 ②：

j++

填空位置 ③：

j

填空位置 ④：

s[i]

题目解析

此题考查简单的字符串处理。delnum就是删数字函数，len是删完的长度，逐个访问字符 s[i]，如果不是数字字符，就是有效字符，保存至s[j]，j是用来记非数字的最后一位。

①空中需要判断当前字符是不是数字，字符为不为数字的条件此处应该为或关系。

②空中需要将i位置上的字符赋值给j位置。这之后需要更新非数字的最后一位的位置，因此需要将j加一。

③空中需要范围处理后的字符串的长度，因此我们需要返回j。

④空我们需要输出最后的结果因此我们需要输出s[i]。
最大子矩阵和）给出 mm 行 nn 列的整数矩阵,求最大的子矩阵和(子矩阵不能为空)。

输入第一行包含两个整数 mm 和 nn，即矩阵的行数和列数。之后 mm 行,每行 nn 个整数，描述整个矩阵。程序最终输出最大的子矩阵和。

1

include [HTML_REMOVED]

2
using namespace std;
3
const int SIZE = 100;
4
int matrix[SIZE + 1][SIZE + 1];
5
int rowsum[SIZE + 1][SIZE + 1]; //rowsum[i][j]记录第 i 行前 j 个数的和
6
int m, n, i, j, first, last, area, ans;
7
int main()
8
{
9
cin >> m >> n;
10
for(i = 1; i <= m; i)
11
for(j = 1; j <= n; j)
12
cin >> matrix[i][j];
13
ans = matrix ①;
14
for(i = 1; i <= m; i)
15
②
16
for(i = 1; i <= m; i)
17
for(j = 1; j <= n; j)
18
rowsum[i][j] = ③;
19
for(first = 1; first <= n; first)
20
for(last = first; last <= n; last)
21
{
22
④;
23
for(i = 1; i <= m; i)
24
{
25
area += ⑤;
26
if(area > ans)
27
ans = area;
28
if(area < 0)
29
area = 0;
30
}
31
}
32
cout << ans << endl;
33
return 0;
34
}题目答案

填空位置 ①：

[1][1]

填空位置 ②：

rowsum[i][0]=0;

填空位置 ③：

rowsum[i][j-1]+matrix[i][j]

填空位置 ④：

area=0

填空位置 ⑤：

rowsum[i][last]-rowsum[i][first-1]

题目解析

本题解决最大子矩阵和所用的算法：计算数组rowsum；枚举子矩阵的左边界first和右边界last，将原问题转化为求解一维的最大子段和问题，用贪心法即可解决。

①因为所求最大子矩阵和所涉及的子矩阵不能为空，必须有一个初值，所以我们需要将ans设置为矩阵的左上角元素，也就是 [1][1][1][1]，取其他单元格的值也可以；

②因为后面要求每行前缀和，所以需要将 00 列清零，用于之后的统计；

③求当前行到当前列的前缀和，使用前缀和的方法统计每行的sum值；

④从first列到last列之间求最大子段和，需要将当前的值初始化为 00；

⑤这里求第i行的first列到last列之间的数值和，这里采用前缀和方法来加速计算过程。