

无符号八位二进制数的表示范围0~2的8次方-1,即0~255,因此选项296和256不在范围之内,还要最大。
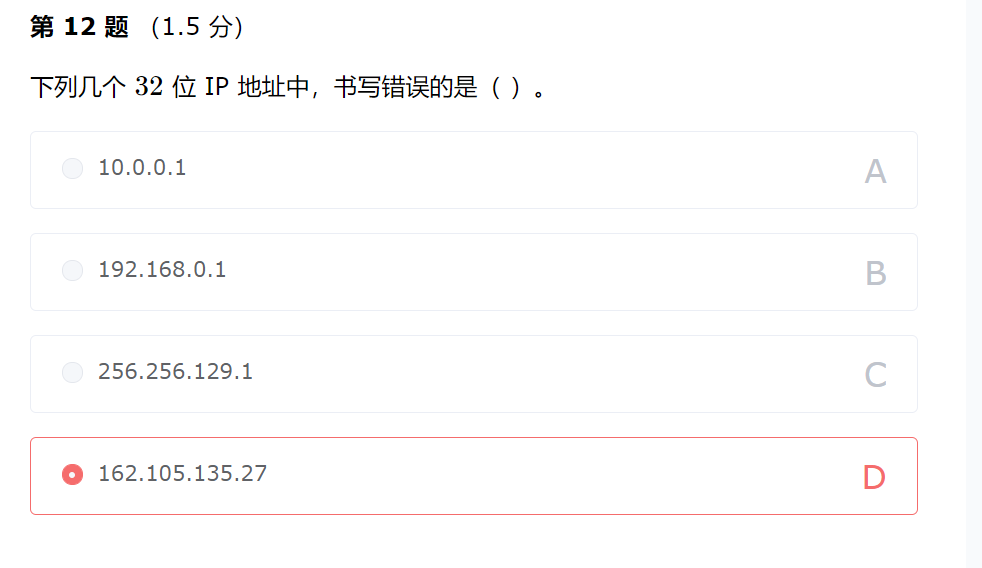
32位IP地址中的4段数据均为八位二进制数,因此每段数字的范围均在0~255.

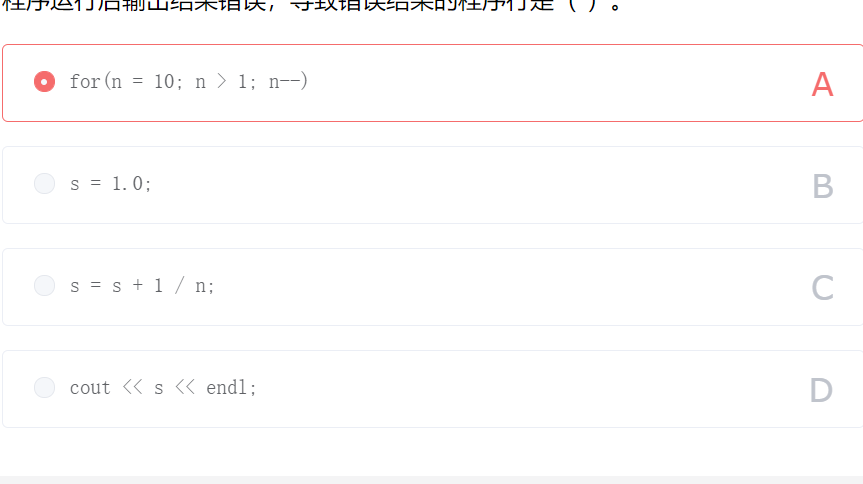
由于n是整数,因此表达式中的1/n会处理为整数除法,而这里我们需要的结果应该为实数。要使结果正确,需要使用实数除法,可以改为1.0/n或1/(float)n等。
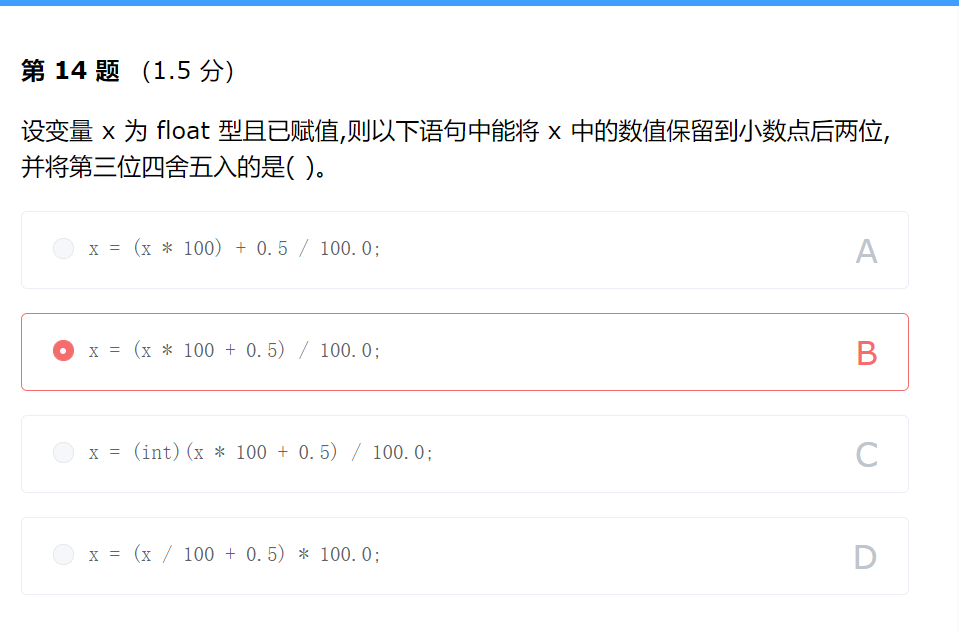
通过将float型强制转换为int型可实现截取整数的操作,而在截取之前加0.5,就实现了四舍五入的功能。本题也可以使用排除法,通过代入具体的数值进行验证。
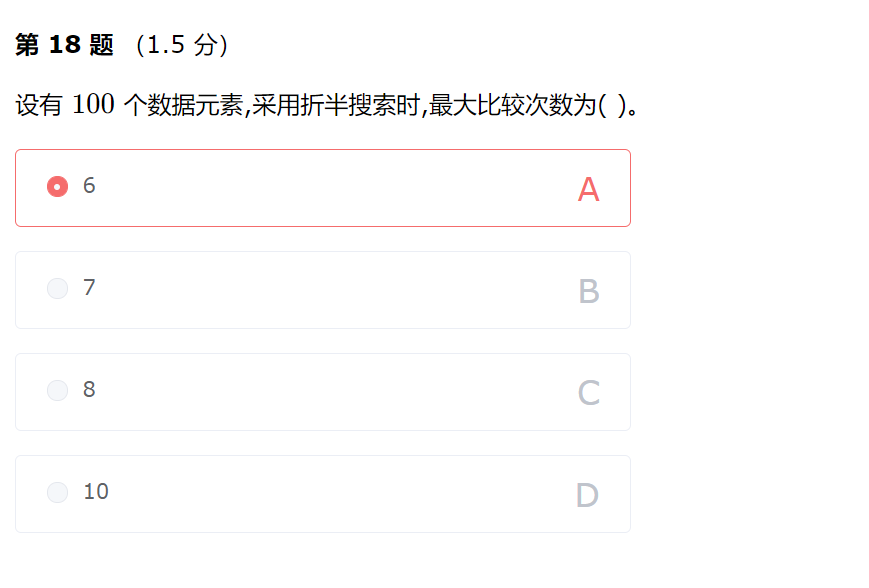
在 2^n-12
n
−1 个元素中采用折半搜索,最大比较次数为 nn 次。而 2^6-1=63<100<127=2^7-12
6
−1=63<100<127=2
7
−1。
26题
#include <iostream>
using namespace std;
const int SIZE = 100;
int main()
{
int p[SIZE];
int n, tot, i, cn;
tot = 0;
cin >> n;
for(i = 1; i <= n; i++)
p[i] = 1;
for(i = 2; i <= n; i++)
{
if(p[i] == 1)
tot++;
cn = i * 2;
while(cn <= n)
{
p[cn] = 0;
cn += i;
}
}
cout << tot << endl;
return 0;
}
此题可以通过直接模拟完成,不过细节比较多容易出错。经过简单的分析或模拟前几步就可以发现,此程序的功能就是用筛法求 nn 以内的质数,输出质数个数。而 3030 以内的质数有 2, 3, 4, 5, 11, 13, 17, 19, 23, 292,3,4,5,11,13,17,19,23,29 共 1010 个。
27题:
#include <iostream>
using namespace std;
int delnum(char *s)
{
int i, j;
j = 0;
for(i = 0; s[i] != '\0'; i++)
if(s[i] < '0' ① s[i] > '9')
{
s[j] = s[i];
②;
}
return ③;
}
const int SIZE = 30;
int main()
{
char s[SIZE];
int len, i;
cin.getline(s, sizeof(s));
len = delnum(s);
for(i = 0; i < len; i++)
cout << ④;
cout << endl;
return 0;
}
题目答案
填空位置 ①:
||
填空位置 ②:
j++
填空位置 ③:
j
填空位置 ④:
s[i]
题目解析
此题考查简单的字符串处理。delnum就是删数字函数,len是删完的长度,逐个访问字符 s[i],如果不是数字字符,就是有效字符,保存至s[j],j是用来记非数字的最后一位。
①空中需要判断当前字符是不是数字,字符为不为数字的条件此处应该为或关系。
②空中需要将i位置上的字符赋值给j位置。这之后需要更新非数字的最后一位的位置,因此需要将j加一。
③空中需要范围处理后的字符串的长度,因此我们需要返回j。
④空我们需要输出最后的结果因此我们需要输出s[i]。
28题:
#include <iostream>
using namespace std;
const int SIZE = 100;
int matrix[SIZE + 1][SIZE + 1];
int rowsum[SIZE + 1][SIZE + 1]; //rowsum[i][j]记录第 i 行前 j 个数的和
int m, n, i, j, first, last, area, ans;
int main()
{
cin >> m >> n;
for(i = 1; i <= m; i++)
for(j = 1; j <= n; j++)
cin >> matrix[i][j];
ans = matrix ①;
for(i = 1; i <= m; i++)
②
for(i = 1; i <= m; i++)
for(j = 1; j <= n; j++)
rowsum[i][j] = ③;
for(first = 1; first <= n; first++)
for(last = first; last <= n; last++)
{
④;
for(i = 1; i <= m; i++)
{
area += ⑤;
if(area > ans)
ans = area;
if(area < 0)
area = 0;
}
}
cout << ans << endl;
return 0;
}
题目答案
填空位置 ①:
[1][1]
填空位置 ②:
rowsum[i][0]=0;
填空位置 ③:
rowsum[i][j-1]+matrix[i][j]
填空位置 ④:
area=0
填空位置 ⑤:
rowsum[i][last]-rowsum[i][first-1]
题目解析
本题解决最大子矩阵和所用的算法:计算数组rowsum;枚举子矩阵的左边界first和右边界last,将原问题转化为求解一维的最大子段和问题,用贪心法即可解决。
①因为所求最大子矩阵和所涉及的子矩阵不能为空,必须有一个初值,所以我们需要将ans设置为矩阵的左上角元素,也就是 [1][1][1][1],取其他单元格的值也可以;
②因为后面要求每行前缀和,所以需要将 00 列清零,用于之后的统计;
③求当前行到当前列的前缀和,使用前缀和的方法统计每行的sum值;
④从first列到last列之间求最大子段和,需要将当前的值初始化为 00;
⑤这里求第i行的first列到last列之间的数值和,这里采用前缀和方法来加速计算过程。

