常识问题，扫描仪、键盘、鼠标均属于输入设备，打印机为输出设备。 链表无法随机访问任意元素，查找任一节点都需要进行复杂度为 \mathcal{O}(n)O(n) 的顺序查找过程。链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域。相比于线性表顺序结构，操作复杂。由于不必须按顺序存储，链表在插入的时候可以达到 \mathcal{O}(1)O(1) 的复杂度，比另一种线性表顺序表快得多，但是查找一个节点或者访问特定编号的节点则需要 \mathcal{O}(n)O(n) 的时间。n 层的满二叉树中节点数为 2^n-12 n−1。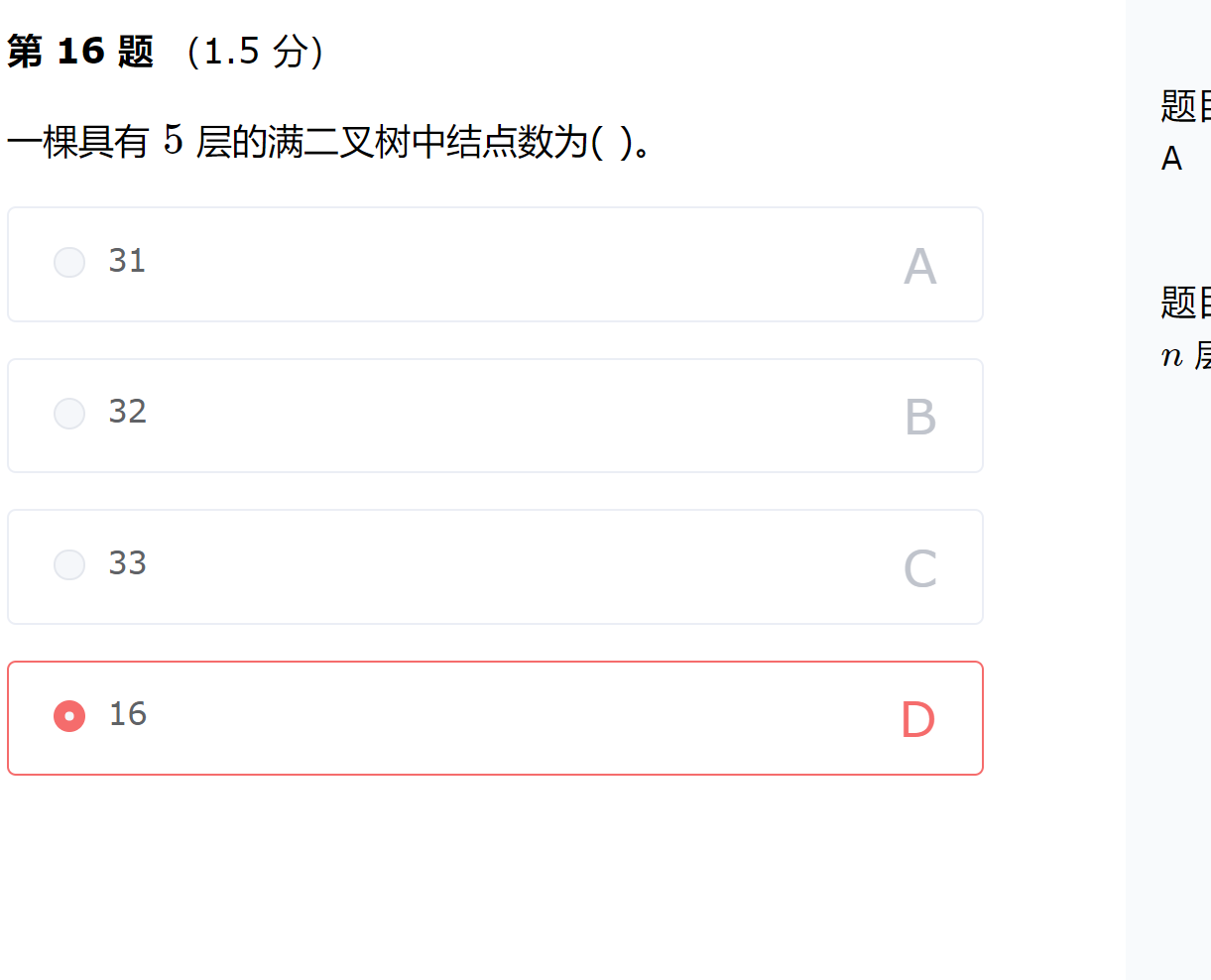 有向图中每个顶点的度分成两种，分别是入度和出度，所有的入度之和与所有的出度之和相等，对于一个顶点来说，该顶点的度等于该顶点的入度与出度之和。

此题考查简单的字符串处理。delnum就是删数字函数，len是删完的长度，逐个访问字符 s[i]，如果不是数字字符，就是有效字符，保存至s[j]，j是用来记非数字的最后一位。

①空中需要判断当前字符是不是数字，字符为不为数字的条件此处应该为或关系。

②空中需要将i位置上的字符赋值给j位置。这之后需要更新非数字的最后一位的位置，因此需要将j加一。

③空中需要范围处理后的字符串的长度，因此我们需要返回j。

④空我们需要输出最后的结果因此我们需要输出s[i]。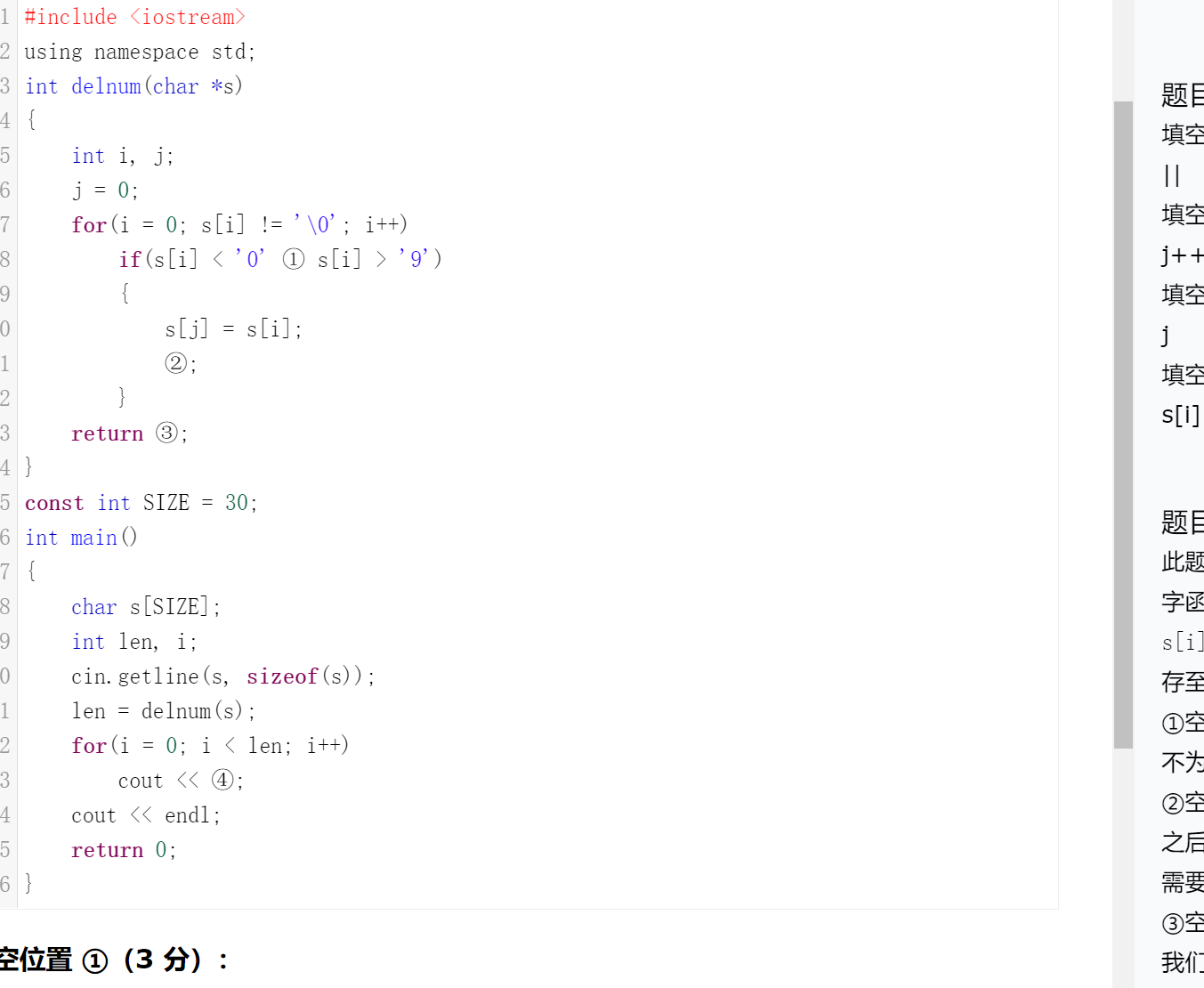
本题解决最大子矩阵和所用的算法：计算数组rowsum；枚举子矩阵的左边界first和右边界last，将原问题转化为求解一维的最大子段和问题，用贪心法即可解决。

①因为所求最大子矩阵和所涉及的子矩阵不能为空，必须有一个初值，所以我们需要将ans设置为矩阵的左上角元素，也就是 [1][1][1][1]，取其他单元格的值也可以；

②因为后面要求每行前缀和，所以需要将 00 列清零，用于之后的统计；

③求当前行到当前列的前缀和，使用前缀和的方法统计每行的sum值；

④从first列到last列之间求最大子段和，需要将当前的值初始化为 00；

⑤这里求第i行的first列到last列之间的数值和，这里采用前缀和方法来加速计算过程。