盒子放球问题集合

球相同，盒不同，没有空盒

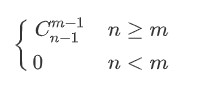
考虑使用隔板法，n个球n-1个空，使用m-1块板子来隔开

球相同，盒不同，允许空盒

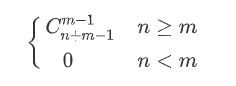
同样使用隔板法，不过在使用隔板法之前每个盒子内先放一个球，即在m+n个球中用m-1个隔板隔开

球不同，盒相同，无空盒

dp[n][m]=m*dp[n-1][m-1]  n<m>=1
dp[k][k]=1 k>=0
dp[k][0]=0 k>=1
0          m>n

考虑第二类斯特林数，dp[x,y]表示符合要求且前x个球放在前y个箱子内的所有方案数

对于第n个球，如果前面n-1个球已经放在了m个箱子里，那么第n个球可以放在任意m个箱子内，因此 dp[n,m]+=dp[n-1,m]*m

如果前面n-1个球已经放在前m-1个箱子里，则第n个球必须放在第m个箱子里，因此dp[n,m]+=dp[n-1,m-1]

边界情况 dp[i,i]=1,其余情况皆为0

球不同，盒相同，允许空盒

$$ \sum dp[n][i] \qquad m\ge i \ge 0 $$

其中的dp[n,m]为上一种情况的第二类斯特林数。在上一种情况的前提下去枚举箱子的个数

球不同，盒不同，无空盒

$$ dp[n][m] \cdot m! $$

dp[n,m]为第三种情况的第二类斯特林数。给和自定义顺序，即再乘一个盒子的排列数

球不同，盒不同，允许空盒

$$ m^n $$

每个球有m种情况，一共n个球

球相同，盒相同，允许空盒

dp[n][m]=dp[n][m-1]+dp[n-m][m]  n>=m
dp[n][m]=dp[n][m-1]  m>n
边界：
    dp[k][1]=1
    dp[1][k]=1
    dp[0][k]=1

dp[n,m]表示有n个球放在m个箱子里

我们可以选择再所有箱子里面都放1个球，也可以不选择这个操作

如果选择就是从dp[n-m,m]转移过来

如果不选择，就是从dp[n,m-1]转移过来

球相同，盒相同，无空盒

dp[n-m][m]=dp[n-m][m-1]+dp[n-2m][m]  n>=2m
dp[n-m][m]=dp[n-m][m-1]  2m>n
0 n<m

因为要求无空盒，现在每个盒子内放入一个球，然后剩下n-m个球，再做一遍球同盒同允许空盒即可