背包问题中的循环

循环物品
$\\quad$循环体积
$\\quad\\quad$循环决策

01背包问题

有$N$件物品和一个容量是$V$的背包。每件物品只能使用一次。第$i$件物品的体积是$v[i]$，价值是$w[i]$。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。

特点：每种物品仅有一件，可以选择放或不放

用子问题定义状态：即 $f[i][j]$ 表示前 $i$ 件物品恰放入一个容量为 $j$ 的背包可以获得的最大价值。则其状态转移方程便是：
$$ f[i][j] = max \{f[i-1][v], f[i-1][j - v[i]] + w[i] \} $$

二维表示：

int n,m, v[N], w[N], f[N][N];

int main( ) 
{
    cin >> n >> m;
    for ( int i=1; i <=n ;i++ ) cin >> v[i] >> w[i];
    /*
       n : 物品数量， m：背包容积
       f[0][0 ~ m] = 0;
    */ 
    for ( int i =1; i<=n; i++ ) 
    {
        for ( int j =0; j <= m; j++ ) 
        {
            // 状态计算的两种情况
            f[i][j] = f[i-1][j]; 
            // 第二种情况 f[i][j] 不一定存在
            if ( j >= v[i] ) f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i] );
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

一维优化：

int main( ) 
{
    cin >> n >> m;
    for ( int i=1; i <=n ;i++ ) cin >> v[i] >> w[i];

    for ( int i =1; i<=n; i++ ) 
        // 注意j从大到小枚举（若从小到大则会枚举重复项）
        for( int j = m; j >= v[i]; j-- ) 
            f[j]= max(f[j], f[j - v[i]] + w[i]);


    cout << f[m] << endl;
    return 0;
}

保证第$i$次循环中的状态$f [i][j]$是由状态$f[i-1][j-w[i]]$递推而来
为了保证每件物品只选一次，保证在考虑“选入第$i$件物品”这件策略时，依据的是一个绝无已经选入第$i$ 件物品的子结果$f[i-1][j-w[i]]$

初始化细节：

求最优解的背包问题题目中，事实上有两种不太相同的问法。有的题目要求”恰好装满背包”时的最优解，有的题目则并没有要求必须把背包装满。这两种问法的区别是在初始化的时候有所不同。

如果是第一种问法，要求恰好装满背包，那么在初始化时除$f[0]$为$0$, 其它$f[1…V]$均设为$-\infty$
这样就可以保证最终得到的$f[N]$是一种恰好装满背包的最优解。

并没有要求必须把背包装满，而是只希望价值尽量大
初始化时应该将$f[0…V]$全部设为$0$。

理由：
初始化的$f$数组事实上就是在没有任何物品可以放入背包时的合法状态。
如果要求背包恰好装满，那么此时只有容量为$0$的背包可能被价值为$0$的$nothing$“恰好装满”，其它容量的背包均没有合法的解，属于未定义的状态，它们的值就都应该是$-\infty$了。
如果背包并非必须被装满，那么任何容量的背包都有一个合法解“什么都不装”，这个解的价值为$0$，所以初始时状态的值也就全部为$0$了。

完全背包问题

有$N$种物品和一个容量是$V$的背包，每种物品都有无限件可用。第$i$种物品的体积是$v[i]$价值是$w[i]$。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

$f[i][j]$表示前$i$种物品恰放入一个容量为$V$的背包的最大权值
状态转移方程：$$ f[i][j] = max \{f[i][j], f[i-1, j - k * v[i]] + k * w[i] \} $$

朴素

for( int i = 1; i <= n; i++ )
{
   for( int j = 0; j <= m; j++)
      for ( int k = 0; k * v[i] <= j; k++ )
         f[i][j] = max(f[i][j], f[i-1][j - k * v[i]] + k * w[i]);
}
cout << f[n][m] << endl;

二维优化

// f[0][0~n] = 0;
    for ( int i = 1; i <= n; i++ ) 
        for ( int j = 0; j <= m; j++ ) {
            f[i][j] = f[i-1][j]; 
            // 01背包从第i-1层转移，完全背包从第i层
            if ( j >= v[i] ) f[i][j] = max(f[i][j], f[i][j-v[i]] + w[i]); 
        }
    cout << f[n][m] << endl;

完全背包的特点恰是每种物品可选无限件，所以在考虑“加选一件第$i$种物品”这种策略时，却正需要一个可能已选入第$i$种物品的子结果$f[i][j−w[i]]$，所以就可以并且必须采用$j=0…V$的顺序循环。
状态转移方程：$$ f[i][j] = max \{ f[i-1][j], f[i][j - v[i]] + w[i] \} $$

一维优化

  for( int i = 1; i <= n; i++)
    for ( int j = v[i]; j <= m; j++ )
        // 由于从第i层转移，所以不需要从大到小枚举避免重复计算
        f[j] = max( f[j], f[j - v[i]] + w[i]);

   cout << f[m];

多重背包问题

有$N$种物品和一个容量是$V$的背包。
第$i$种物品最多有$s[i]$件，每件体积是$v[i]$，价值是$w[i]$。
求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

题目和完全背包问题类似。只需将完全背包问题的方程略微修改
因为对于第$i$种物品有$s[i] + 1$种策略：取$0$件，取$1$件……取$s[i]$件。令$f[i][j$]表示前$i$ 种物品恰放入一个容量为$j$的背包的最大权值，
则有状态转移方程：$$ f[i][j] = max \{f[i][j], f[i-1, j - k * v[i]] + k * w[i] \} $$

朴素 $O(NSV)$

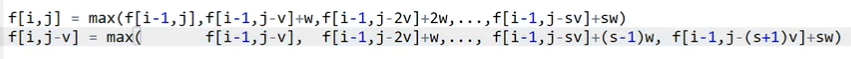
// f[0][0~n] = 0;
    for ( int i=1; i<=n; i++ ) 
        for ( int j=0; j<=m; j++ ) 
            for ( int k=0;k <= s[i] && k*v[i] <= j; k++ ) 
              f[i][j] = max(f[i][j], f[i-1][j-v[i]*k] + w[i]*k);

    cout << f[n][m] << endl;

二进制优化 $O(NlogSV)$

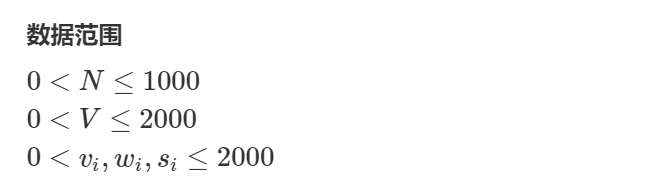
二进制思想：
二进制的思想，我们考虑把第$i$种物品换成若干件物品，使得原问题中第$i$种物品可取的每种策略——取$0…s[i]$件——均能等价于取若干件代换以后的物品。另外，取超过$s[i]$件的策略必不能出现。

将第$i$种物品分成若干件物品，其中每件物品有一个系数，这件物品的体积和价值均是原来的体积和价值乘以这个系数。使这些系数分别为$1,2,4,…,2^{k-1},s[i]-2^{k}+1$，且$k$是满足$s[i]-2^{k}+1>0$的最大整数。
例如，如果$s[i]$为$13$，就将这种物品分成系数分别为$1,2,4,6$的四件物品。分成的这几件物品的系数和为$s[i]$，表明不可能取多于$s[i]$件的第$i$种物品。另外这种方法也能保证对于$0…s[i]$间的每一个整数，均可以用若干个系数的和表示，这个证明可以分$0…2^{k}−1$和$2^{k}…s[i]$两段来分别讨论得。
这样就将第$i$种物品分成了$O(log(s[i]))$种物品，将原问题转化为了复杂度为$O(V∗Σlog(s[i]))$的01背包问题

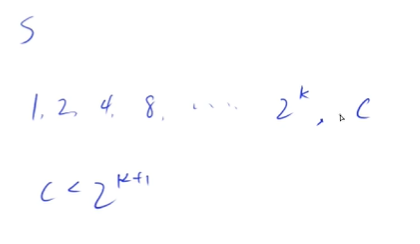
cin >> n >> m;
    int cnt = 0; // 存储打包的数量，表示编号
    for ( int i=1; i<=n; i++ ) {
        int a,b,s; // 体积，价值，数量
        cin >> a >> b >> s;
        int k =1;
        // 将S分解成logS个数，使用二进制优化打包
        // 新打包成的每一堆物品都只能用一次
        while ( k <= s ) {
            cnt++;
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }
        if ( s > 0 ) {
            cnt++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }
    n = cnt;
    for ( int i=1; i<=n; i++ ) {
        for ( int j=m; j>=v[i]; j-- ) {
           f[j] = max( f[j], f[j-v[i] ]  + w[i] );
        }
    }
    cout << f[m] << endl;

单调队列优化 $O(NV)$

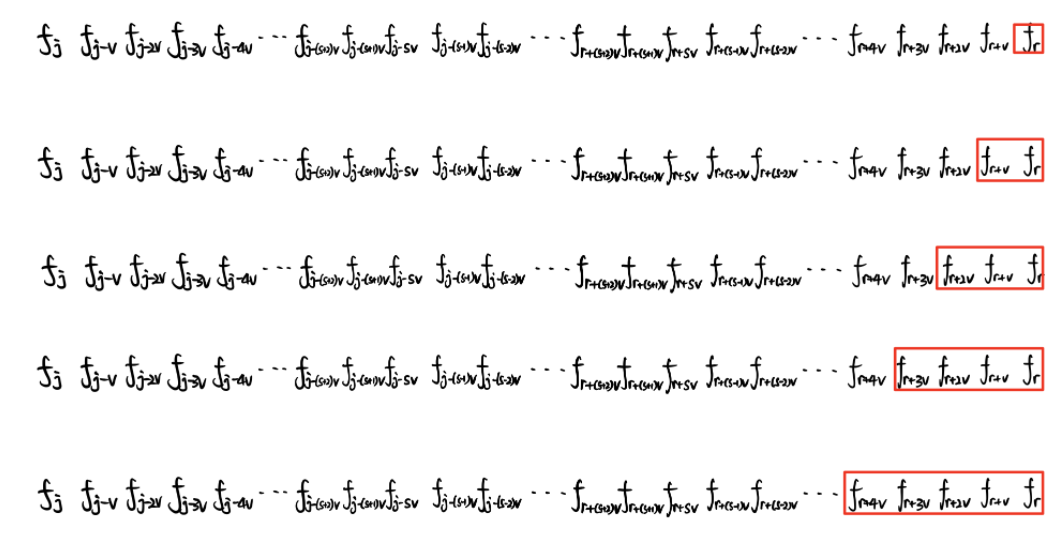
const int N=20010;

int f[N],g[N],q[N];
//f存储的是第i层,g存储第i-1层; q存储的是f,g数组中的下标(体积,例如:q[5]=r+3v), 表示单调队列;

int main()
{
    int n,m;
    scanf("%d%d",&n,&m);

    for(int i = 1;i <= n;i++)
    {
        int v,w,s;
        scanf("%d%d%d",&v,&w,&s);

        memcpy(g,f,sizeof(f));//复制上一层的结果
        for(int r = 0;r < v;r++)//枚举余数
        {
            //tt代表队尾,hh代表对头(最前面的元素)
            int tt = -1,hh = 0;
            //枚举体积,单调队列模板
            for(int j = r; j <= m; j += v)
            {
                //判断是否超出了s件物品;
                while(hh <= tt && q[hh] < j-s*v ) ++hh;
                /*
                如果q[hh]恰好等于r的话,j=s*v+r时,j-s*v=r,此时正好有s个物品
                q[hh]=j-s*v,如果有s+1个物品时,j=(s+1)*v+r-s*v=r+v,大于r,就
                超过了物品范围范围;r+2v同理,如果j=(s+2)+r是则正好有s件物品
                通过等式,如果j=(s+3)v+r则有s+1间物品,无法通过等式.
                */
                while(hh <= tt && g[q[tt]]-(q[tt]-r) / v * w <= g[j]-(j-r)/v*w) --tt;
                //将前面推导出来的公式进行比较
                q[++tt]=j;
                /*
                因为f[j]=max(g[j],g[j-v]+w,····)其中g[j]也是需要参与的,所以更新应放在
                前面,否则如果g[j]恰好是最大的的方案,那么会导致结果的错误;
                */
                f[j]=g[q[hh]]+(j-q[hh])/v*w;//更新最大的值
            }
        }
    }
    cout<<f[m]<<endl;//输出最终结果
    return 0;
}

分组背包问题

有$N$组物品和一个容量是$V$的背包。每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是$v_{ij}$, 价值是 $w_{ij}$，其中$i$是组号，$j$是组内编号。
求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

第一行有两个整数$N$，$V$，用空格隔开，分别表示物品组数和背包容量。
有$N$组数据：

• 每组数据第一行有一个整数$S_{i}$，表示第$i$个物品组的物品数量；
• 每组数据接下来有$S_{i}$行，每行有两个整数$v_{ij}$, $w_{ij}$，用空格隔开，分别表示第$i$个物品组的第$j$ 个物品的体积和价值；

这个问题变成了每组物品有若干种策略：是选择本组的某一件，还是一件都不选。也就是说设$f[i][j]$表示前$i$组物品花费空间$j$能取得的最大权值
状态转移方程：$$ f[i][j] = max \{ f[i][j], f[i-1][j - v[i][k] + w[i][k] \} $$

cin >> n >> m;
    for ( int i=1; i<=n; i++ ) 
    {
        cin >> s[i]; // 物品数量
        for ( int j=0; j<s[i]; j++ ) 
            cin >> v[i][j] >> w[i][j];
    }
    for ( int i=1; i<=n; i++ ) 
        for ( int j = m; j >=0; j-- ) 
            for ( int k=0; k < s[i]; k++ ) 
                if ( v[i][k] <= j ) 
                   f[j] = max( f[j], f[j - v[i][k]] + w[i][k] ); 
    cout << f[m] << endl;

$for(j…0)$这一层循环必须在$for$(所有的$i$属于组$k$)之外。这样才能保证每一组内的物品最多只有一个会被添加到背包中。

混合背包问题

有$N$种物品和一个容量是$V$的背包。

物品一共有三类：
第一类物品只能用$1$次（01背包）；
第二类物品可以用无限次（完全背包）；
* 第三类物品最多只能用 $s_{i}$ 次（多重背包）；

每种体积是$v_{i}$，价值是$w_{i}$。
求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

第一行两个整数,$N$,$V$，用空格隔开，分别表示物品种数和背包容积。

接下来有$N$行，每行三个整数$v_{i}$,$w_{i}$,$s_{i}$，用空格隔开，分别表示第 i 种物品的体积、价值和数量。

• $s_{i} = -1$ 表示第$i$种物品只能用$1$次；
• $s_{i} = 0$ 表示第$i$种物品可以用无限次；
• $s_{i} = 0$ 表示第$i$种物品可以使用$s_{i}$次；

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
const int N = 1010;
struct Thing
{
    int kind; // 表示种类
    int v,w; // 体积，价值
};
int f[N];
vector<Thing> things;
int n,m;
int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i ++ )
    {
        int v,w,s;
        cin >> v >> w >> s;
        if(s < 0) things.push_back({-1, v, w}); // 01背包
        else if( s == 0 ) things.push_back({0, v, w}); // 多重背包
        else {
            // 混合背包，二进制拆解为01背包问题
            for ( int k = 1; k <= s; k *= 2)
            {
                s -= k;
                things.push_back({-1, v*k, w*k});
            }
            if( s > 0 ) things.push_back({-1, v*s, w*s});
        }
    }
    for(auto thing : things )
    {
        // 01背包求解
        if( thing.kind < 0 )
        {   
            for( int j = m; j >= thing.v; j-- ) f[j] = max(f[j], f[j - thing.v] + thing.w);
        }
        else
        {
        // 完全背包求解   
            for( int j = thing.v; j <= m; j++ ) f[j] = max(f[j], f[j - thing.v] + thing.w);

        }
    }
    cout << f[m];
}

二维费用的背包问题

有$N$件物品和一个容量是$V$的背包，背包能承受的最大重量是$M$。

每件物品只能用一次。体积是$v_{i}$，重量是$m_{i}$，价值是$w_{i}$。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，总重量不超过背包可承受的最大重量，且价值总和最大。
输出最大价值。

设$f[i][j][k]$表示前$i$件物品付出两种代价分别为$j$和$k$时可获得的最大价值
状态转移方程：$$ f[i][j][k] = max \{ f[i-1][j][k], f[i-1][j - v[i]][k - m[i]] + w[i] \} $$

#include <bits/stdc++.h>
using namespace std;
int n, V, M;
const int N = 10010;
int v[N], m[N], w[N], f[N][N];

signed main () {
    cin >> n >> V >> M; // 最大体积，重量
    for (int i = 1; i <= n; i ++) {
        cin >> v[i] >> m[i] >> w[i];
    }
    for (int i = 1; i <= n; i ++)
        for (int j = V; j >= v[i]; j --)
            for (int k = M; k >= m[i]; k --)
                f[j][k] = max (f[j - v[i]][k - m[i]] + w[i], f[j][k]);
    cout << f[V][M];
} 

有依赖的背包问题

有$N$个物品和一个容量是$V$的背包。

物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。

如下图所示：

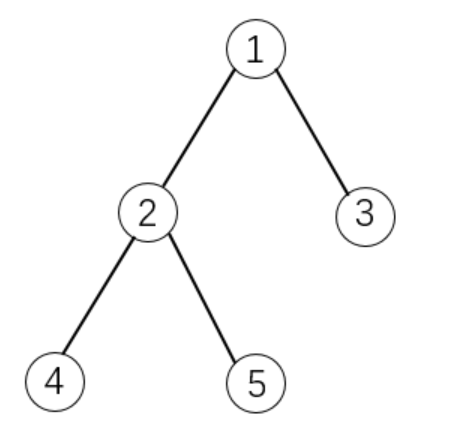
如果选择物品$5$，则必须选择物品$1$和$2$。这是因为$2$是$5$的父节点，$1$是$2$的父节点。
每件物品的编号是$i$，体积是$v_{i}$，价值是$w_{i}$，依赖的父节点编号是$p_{i}$。物品的下标范围是$1…N$。
求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

这种背包问题的物品间存在某种“依赖”的关系。也就是说，$i$依赖于$j$，表示若选物品$i$，则必须选物品$j$

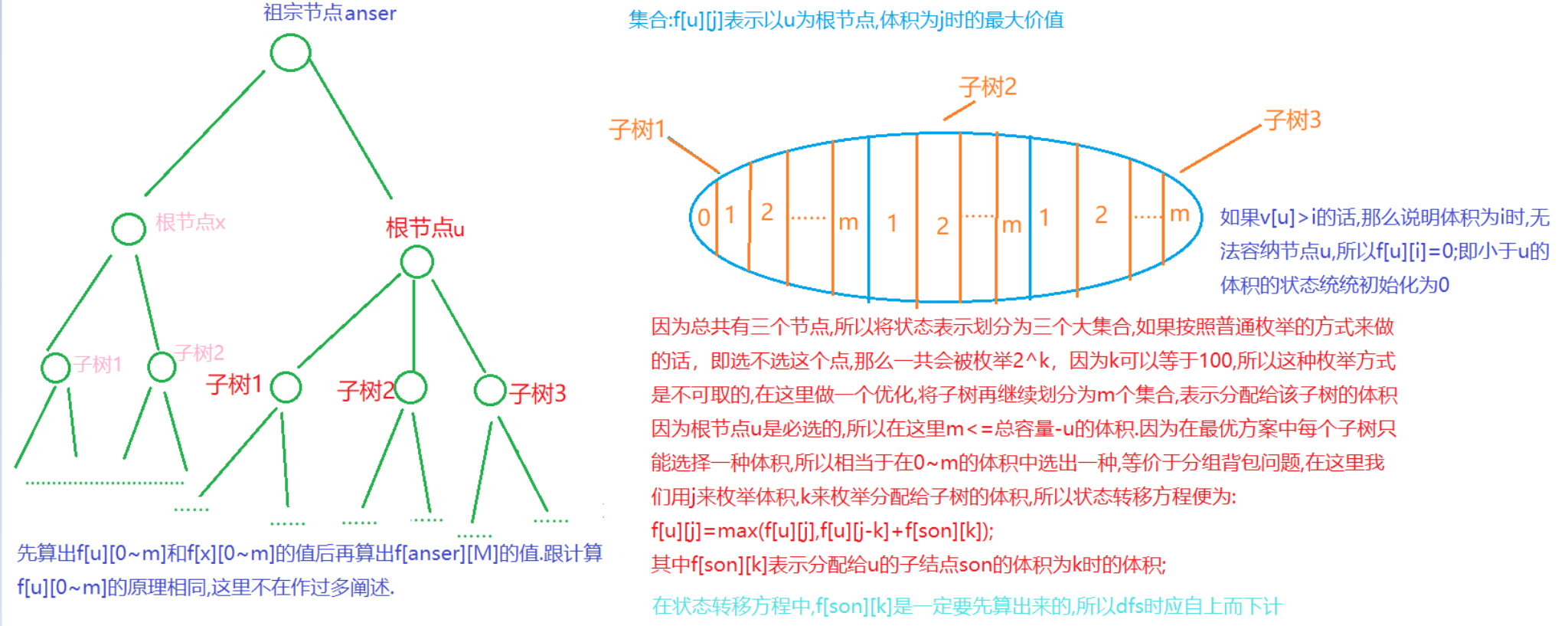
const int N=110;
int f[N][N],v[N],w[N],h[N],ne[N],e[N],idx;
int n,m;
void add(int a,int b)//a是b的父节点
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u)//因为u是根节点,所以u是必选的
{
    for(int i=h[u];i!=-1;i=ne[i])//枚举子树
    {
        int son=e[i];//记录子树的根节点
        dfs(e[i]);//因为dfs是自下而上的,所以需要从下到上计算

        for(int j=m-v[u];j>=0;j--)//因为u是该树的根节点,所以必选,预留出u的空间
         for(int k=0;k<=j;k++)//枚举该子树分配到的体积
         f[u][j]=max(f[u][j],f[u][j-k]+f[son][k]);//加上该子树的值
    }
    //把物品u加进去,因为是根节点
    for(int i=m;i>=v[u];i--) f[u][i]=f[u][i-v[u]]+w[u];
    for(int i=0;i<v[u];i++) f[u][i]=0;//如果无法容纳物品u,那他的价值为0;
}
int main()
{
    memset(h,-1,sizeof(h));
    scanf("%d%d",&n,&m);

    int anser;
    for(int i=1;i<=n;i++)
    {
        int p;
        scanf("%d%d%d",&v[i],&w[i],&p);

        if(p==-1) anser=i;//寻找出祖宗节点
        else add(p,i);
    }
    dfs(anser);
    printf("%d",f[anser][m]);
    return 0;
}

背包问题求方案数

有$N$件物品和一个容量是$V$的背包。每件物品只能使用一次。
第$i$件物品的体积是$v_{i}$，价值是$w_{i}$。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最优选法的方案数。注意答案可能很大，请输出答案模 $10^{9}+7$ 的结果。

#include<iostream>
using namespace std;
const int N = 1010;
const int mod = 1e9 + 7;
int f[N], cnt[N];
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for(int i = 0; i <= m; i ++)  cnt[i] = 1;

    for(int i = 1; i <= n; i ++)
    {
        int v, w;
        scanf("%d%d", &v, &w);
        for(int j = m; j >= v; j --)
        {
            int value = f[j - v] + w;
            if(value > f[j])
            {
                f[j] = value;
                cnt[j] = cnt[j - v];
            }
            else if( value == f[j] )
                cnt[j] = (cnt[j] + cnt[j - v]) % mod;
        }
    }
    printf("%d", cnt[m]);
    return 0;
}

背包问题求具体方案 ——> 最短路问题求路径

有$N$件物品和一个容量是$V$的背包。每件物品只能使用一次。

第$i$件物品的体积是$v_{i}$，价值是$w_{i}$。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出字典序最小的方案。这里的字典序是指：所选物品的编号所构成的序列。物品的编号范围是$1…N$。

输出最小字典序：

1.可选可不选则必选
2.不可选则不选
3.只能选则选

const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for( int i = 1; i <= n; i++ )
      scanf("%d%d", &v[i], &w[i]);

    for( int i = n; i >= 1; i-- )
      for( int j = 0; j <= m; j++ )
      {
          f[i][j] = f[i + 1][j];
          if( j >= v[i]) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
      }
    // f[1][m] -> max_val
    int j = m;
    for( int i = 1; i <= n; i++ )
      if(j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i])
      {
          cout << i << " ";
          j -= v[i];
      }

    return 0;

}