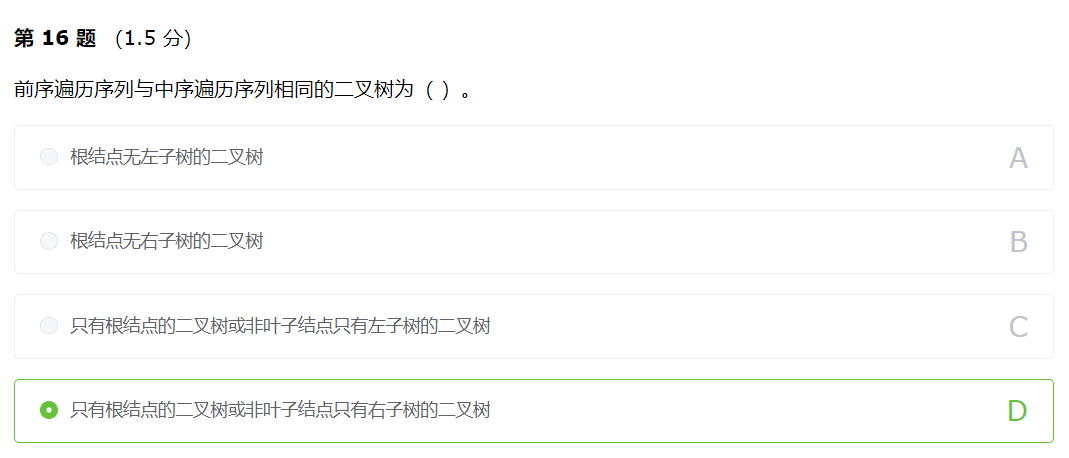
解析：要使前序遍历序列与中序遍历序列相同，对于任意非叶子结点，不能存在左子树，否则前序遍历序列与中序遍历序列不可能相同。除此之外，只有根结点的二叉树，前序、中序、后序遍历都相同。

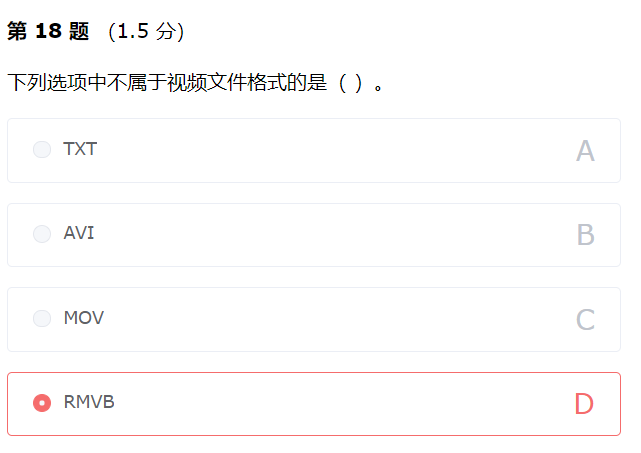
解析：TXT 格式是纯文本格式。其余均为常见视频文件格式。

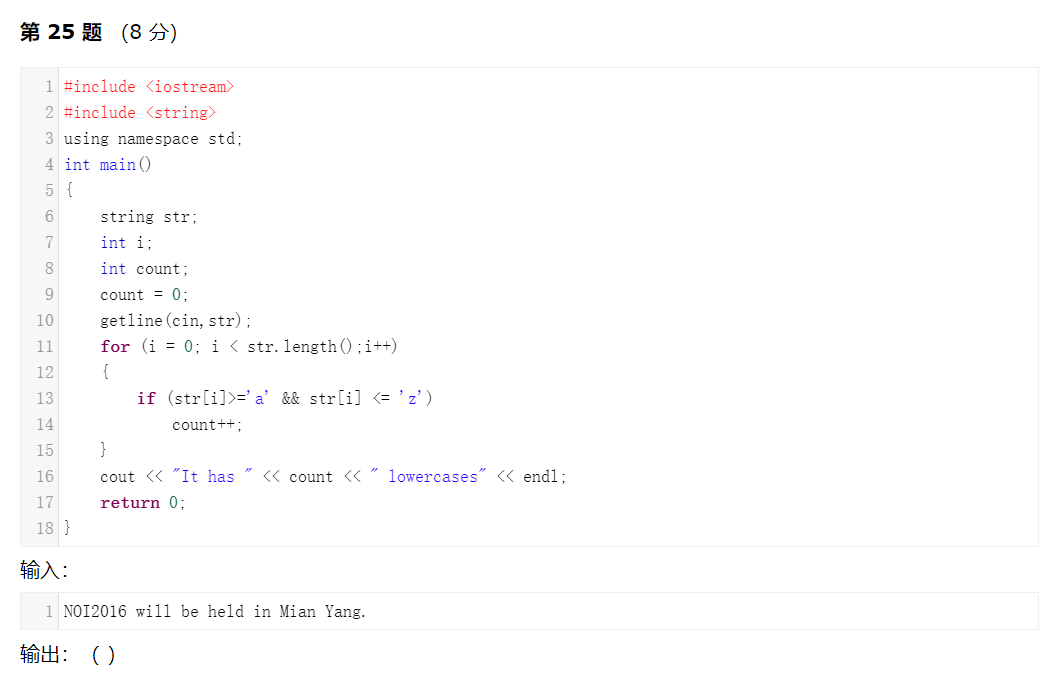
解析：这个程序统计了字符串中小写字母的个数。注意不要遗漏提示信息或写错提示信息。

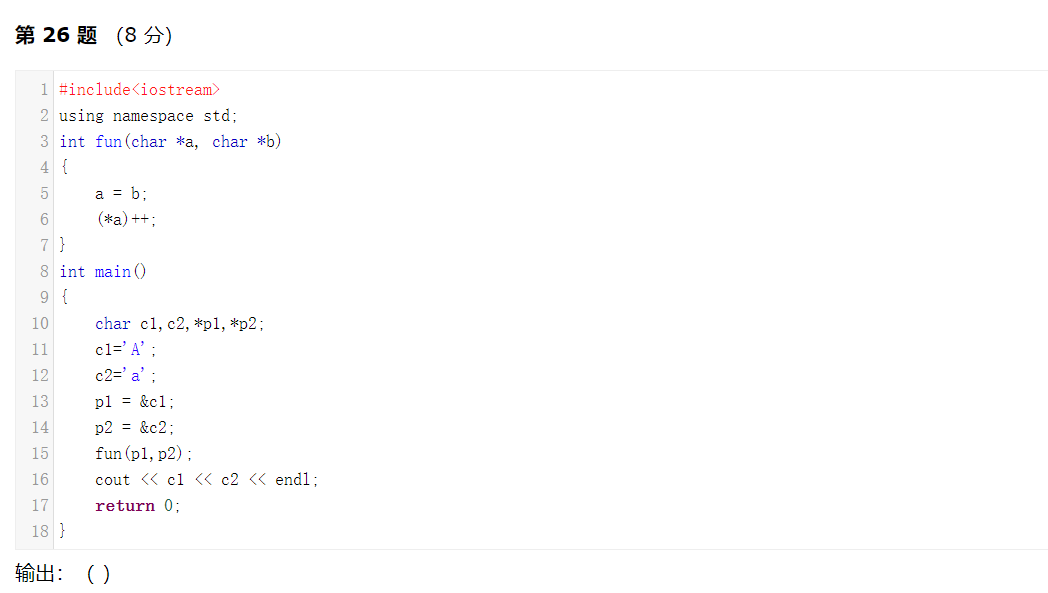
解析：本题考查指针的应用。要注意p1，p2，a，b都是指针，a=b是指将b指向的地址赋值给a，既让a指向b所指向的地址，(*a)，是将a指向的地址里的东西+1。这个时候的a指向c2的地址，所以(*a)，会使得 c2 = a + 1 = b。

#include<iostream>
using namespace std;
const int dayNum[]={-1,31,28,31,30,31,30,31,31,30,31,30,31};
int m, offset, i;
int main()
{
    cin >> m;
    cout <<"S   M   T   W   T   F   S"<<endl;//'    '为tab制表符
    ①;
    for (i = 1; i < m; i++)
        offset = ②;
    for (i = 0; i < offset; i++)
        cout <<'    ';
    for (i = 1; i <= ③;i++)
    {
        cout << ④;
        if(i==dayNum[m]||⑤==0)
            cout << endl;
        else
            cout << '   ';
    }
    return 0;
}

解析：通过偏移数offset将每个月的日期输出到对应的星期上。
空①，offset记录上个月的偏移数，1月份的偏移数为4，所以此空应填：offset=4
空②，计算第m个月的偏移数，所以应加上前一个月的天数并对7取余数，(offset+dayNum[i])%7
空③，输出第m个月的日期，dayNum[m] 空④，输出循环变量i表示的日期
空⑤，换行条件，当前日期加上偏移数如果是7的倍数时换行，所以应填入：(offset+i)%7

#include <iostream>
using namespace std;
const int MAXN = 1000;
int n,i,lbound,rbound,mid,m,count;
int x[MAXN];
int main()
{
    cin >> n >> m;
    for(i = 0; i < n; i++)
        cin >> x[i];
    lbound = 0;rbound = m;
    while(①) {
        mid=(lbound+rbound)/2;
        ②;
        for(i = 0; i < n; i++)
        {
            if(③)
                ④;
        }
        if(count > n/2)
            lbound = mid + 1;
        else
            ⑤;
    }
    cout << rbound << endl;
    return 0;
}

解析：

二分搜索求中位数。lbound和rbound即中位数的左右边界。
空①，二分搜索的循环条件，即lbound<rbound
空②，count记录x[]中比中位数mid大的数的个数，此时应该初始化为0，所以此空应填入count=0。
空③，if(count > n/2) lbound = mid + 1;表示：如果count的个数超过了一半，再到更大的值区间中搜索中位数，即mid不够大。所以此空应填入x[i]>mid。
空④，count++
空⑤，count <= n/2，到更小的值空间搜索，此时rbound=mid。

附加：

二叉树的基本性质：
性质1：在二叉树的第h层上有2的h-1次方个节点（h>=1）
性质2：深度为h的二叉树有2的h次方-1个节点（h>=1）
性质3：对于一颗非空的二叉树来说， 如果叶子结点数为n0，度数为2的结点数为n2，则有n0＝n2＋1
性质4：当完全二叉树的节点有n个时，深度为log以2为底n的对数向下取整+1
性质5：完全二叉树的编号：
（1）完全二叉树中任何一层最左的节点编号n，则其左子树为2n,右子树为2n+1
（2）完全二叉树中任意一节点编号n,则其左子树为2n,右子树为2n+1

错排问题公式：f(n)=(n−1)×[f(n−1)+f(n−2)]

解析：制作不易，打赏全靠自觉