重点整理：
1.
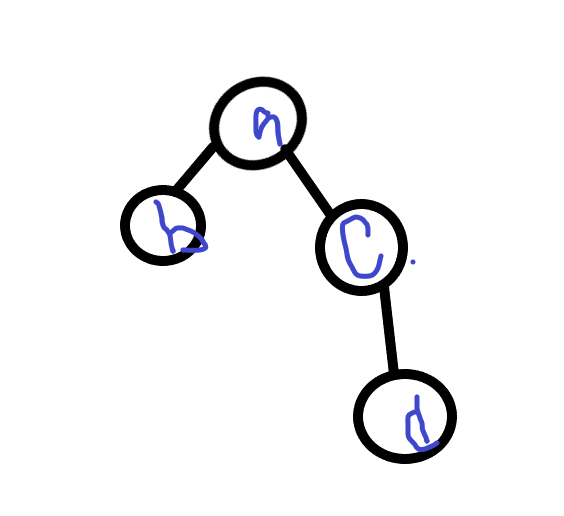
2.二叉树特点：
（1）满二叉树当它的高度为h时，它一共有2的h-1次方个叶子节点。
（2）满二叉树当它的高度为h时，它一共有2的h次方-1个节点。
（3）任意一颗二叉树，它都具备n0=n2-1,的特性。
（4）完全二叉树的左子节点等于根节点2，右子节点等于根节点2+1。根节点等于左子节点或者右子节点/2。
（5）完全二叉树假设二叉树有n个节点它层数的计算方法：算2的x小于等于n。如果小于n-1，层数就是x+1，如果等于n-1层数就是x。
错题：

二进制转十六进制，四位一转，如果不够位，在小数点后补位，补完位后0.1000转十六进制为0.8 A

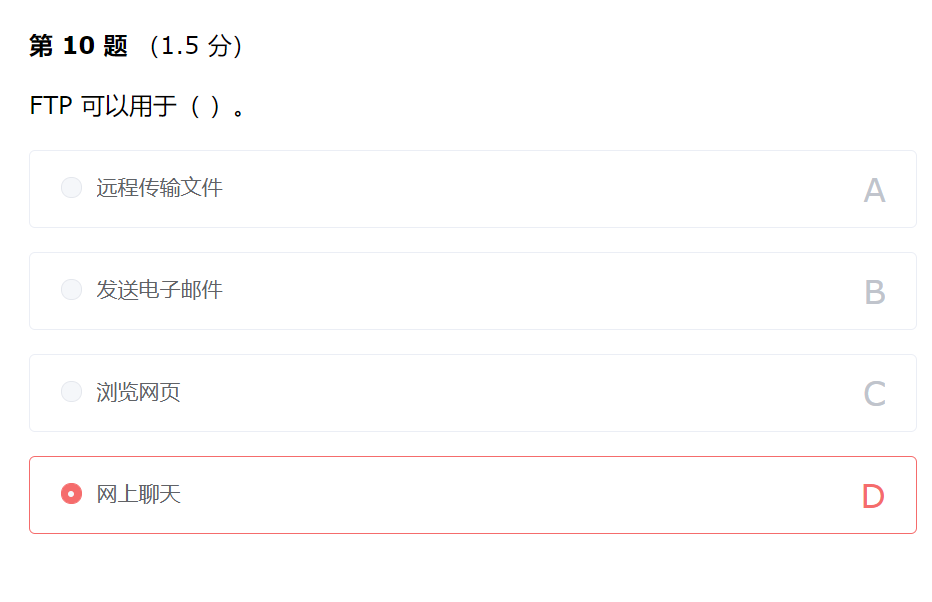
FTP是文件传输协议的简称，中文简称为“文件协议”，用于Internet上的控制文件的双向传输。 A

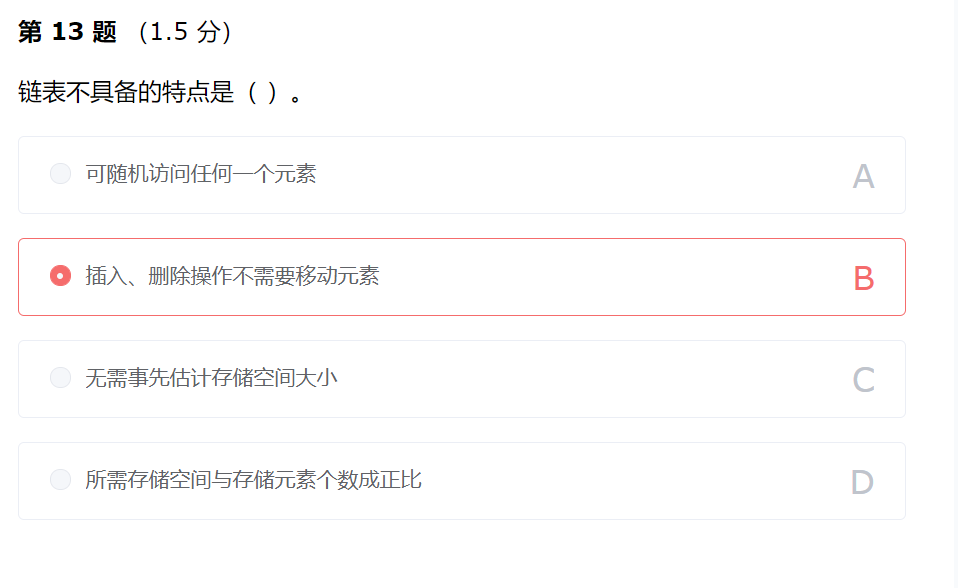
链表无法随机访问任意元素，查找任一节点都需要进行复杂度为o(n)的顺序查找过程。

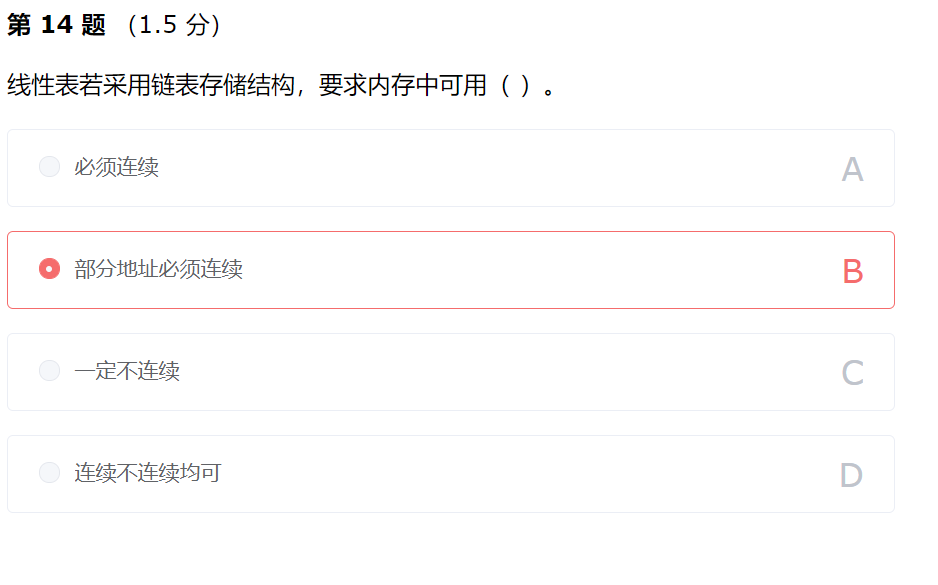
考察数据结构基础知识。数组存储单元地址要连续，而链表可以在产生新结点的时候动态申请内存（不一定连续），也可以事先申请一部分连续的内存来给未来新增的结点预留空间。链表存储单元地址连续或者不连续都可以。

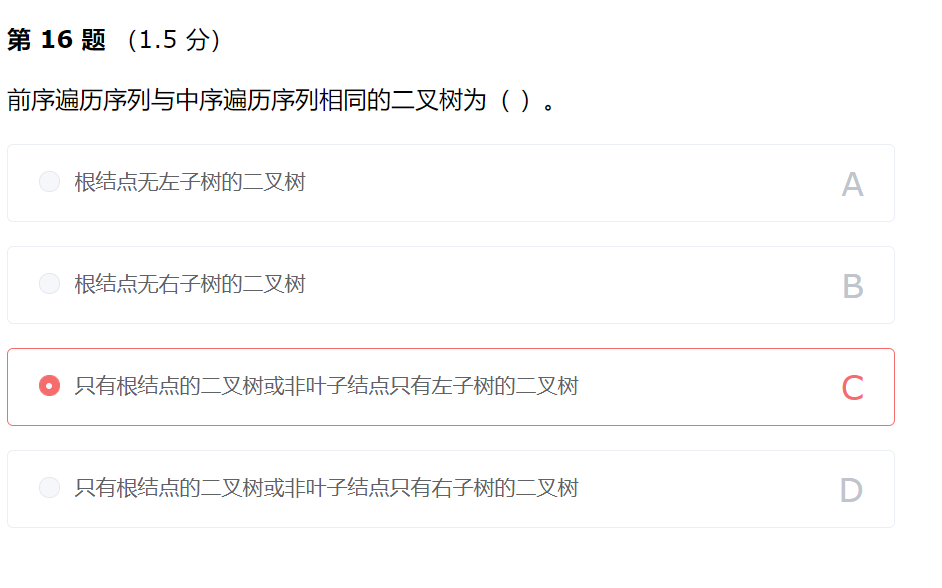
前序遍历的顺序依次为“根结点-左子树-右子树”，中序遍历的顺序依次为“左子树-根结点-右子树”。所以当二叉树只有根结点或非叶子结点只有右子树时，前序遍历和中序遍历的顺序都退化成了：根、右子树，故二者得到的序列相同。要使中序遍历序列与前序遍历序列相同，每个非叶子结点都不能有左子树。

#include<iostream>
using namespace std;
const int dayNum[]={-1,31,28,31,30,31,30,31,31,30,31,30,31};
int m, offset, i;
int main()
{
    cin >> m;
    cout <<"S   M   T   W   T   F   S"<<endl;//'    '为tab制表符
    ①;
    for (i = 1; i < m; i++)
        offset = ②;
    for (i = 0; i < offset; i++)
        cout <<'    ';
    for (i = 1; i <= ③;i++)
    {
        cout << ④;
        if(i==dayNum[m]||⑤==0)
            cout << endl;
        else
            cout << '   ';
    }
    return 0;
}

题目答案：
1：offset=4
2:(offset+dayNum[i])%7
3:dayNum[m]
4:i
5:(offset+i)%7
题目解析：
首先我们看到较为简单的第三四两空，这两空对应的过程显然就是输出日历了。for循环内应该是对每一天输出一个日期，因此循环范围就应该是这个月的天数，也就是dayNum[m]。什么时候应该输出换行符呢？要么就是输出了一个星期之后进行换行，所以这里对应的就是每个星期结束，也就是当i为7的倍数时进行换行。下面再回过来看前两空。通过上面一个for循环可以看出来这个offset是用来控制月历开始的时候要输出多少的空位，再参照题目给出的第一个月的月历就可以知道offset初值应该是4，即第一个空对应需要做的事情。但是这个offset只是对于第一个月正确，因此需要再加上所有小于1月的月份的天数，计算offset的方法就是(offset+dayNum)%7。

#include <iostream>
using namespace std;
const int MAXN = 1000;
int n,i,lbound,rbound,mid,m,count;
int x[MAXN];
int main()
{
    cin >> n >> m;
    for(i = 0; i < n; i++)
        cin >> x[i];
    lbound = 0;rbound = m;
    while(①) {
        mid=(lbound+rbound)/2;
        ②;
        for(i = 0; i < n; i++)
        {
            if(③)
                ④;
        }
        if(count > n/2)
            lbound = mid + 1;
        else
            ⑤;
    }
    cout << rbound << endl;
    return 0;
}

题目答案：
1：lbound[HTML_REMOVED]mid
4:count++
5:rbound=mid
题目解析：
这是一道经典的左闭右闭的二分题，整个题目的过程为：先二分答案，再遍历整个数组验证。第一空是二分的条件，所以应该为lbound<rbound。第二空应该是将计数器count初始化操作，第三空、第四空就对应着统计大于（或小于）mid的数值个数的条件与过程，第五空则是调整右边界，可以参照左边界的调整方法仿写rbound=mid。