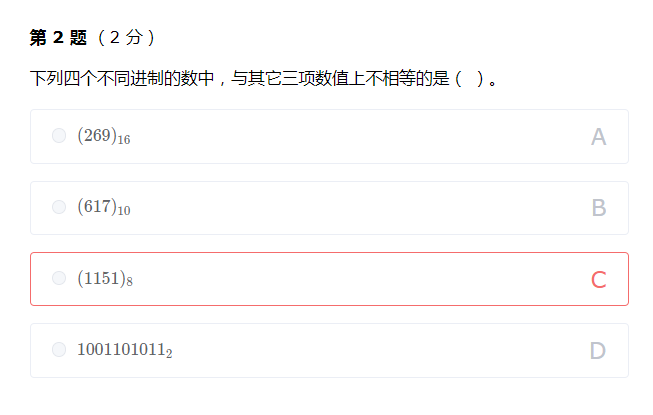
题目答案
D
题目解析
可以将所有数全部转化为十进制,(269){16}(269)
16
,(617){10}(617)
10
,(1151)_8(1151)
8
均为 617617,因此选择 1001101011_21001101011
2
(619619)。
但是,此题更加简单的做法是全部转化为二进制:对于 1616 进制的数,转化为二进制只需要将每一数位的数转写为四位二进制数。
比如说,(269){16}=>(0010|0110|1001) 2=>(1001101001) 2(269)
16
=>(0010∣0110∣1001)
2
=>(1001101001)
2
。
类似的,八进制数转化为二进制的做法是将每一位数字对应转化为三位二进制数,所以 (1151) 8 => (001|001|101|001) 2 => (1001101001) 2(1151)
8
=>(001∣001∣101∣001)
2
=>(1001101001)
2
。这样可以降低运算量。
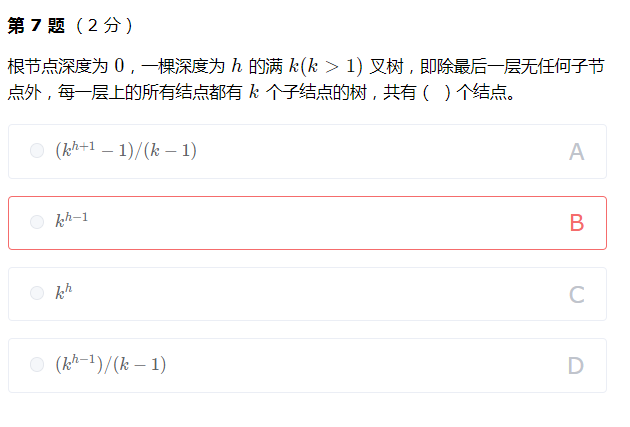
题目答案
A
题目解析
考查数据结构基本知识,对于 kk 叉树,每一层的结点个数依次为 11,kk,k^2k
2
,…,k^hk
h
。
由等比数列求和公式可知,答案为 (k^{h+1}-1)/(k-1)(k
h+1
−1)/(k−1)。此外,本题可以通过画二叉树,三叉树来排除选项。
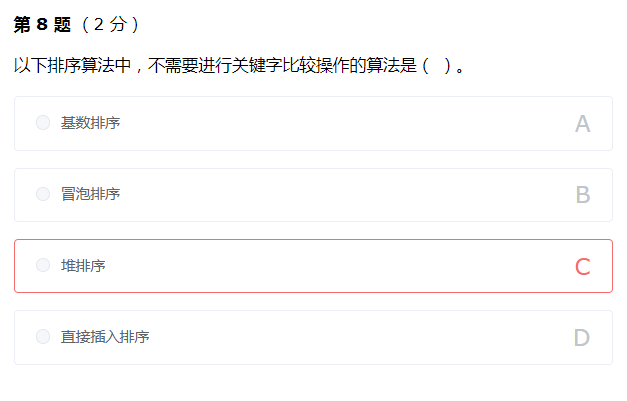
题目答案
A
题目解析
冒泡排序、堆排序和插入排序都是基于两两元素关键字比较的排序。基数排序是直接将元素通过某些规则放到数组的相应位置,不是基于两两元素关键字比较的排序。

题目答案
A
题目解析
考察图论基础知识。
连通图指的是两个点之间都有路径可以到达。
简单图既不含平行边也不含自环的图。
无向图指的是图中的边是无向边。
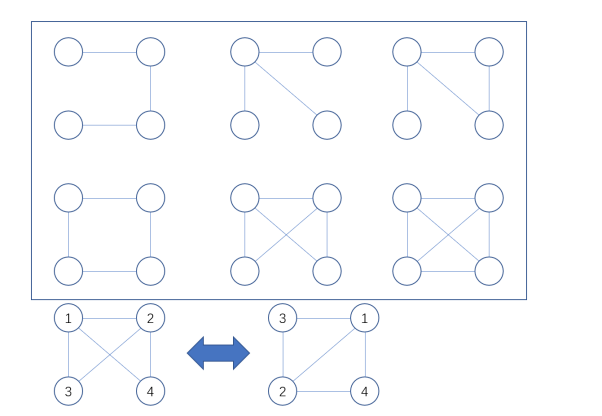
枚举可得有 66 种由 44 个没有区别点构成的不同结构的简单无向连通图。
三条边的图有两个(长为 33 的路、星图)。
四条边的图有两个(圈、三角形加一条边)。
五条边的图有一个(完全图挖掉一条边)。
六条边的图有一个(即 44 个点的完全图)。
题目答案
B
题目解析
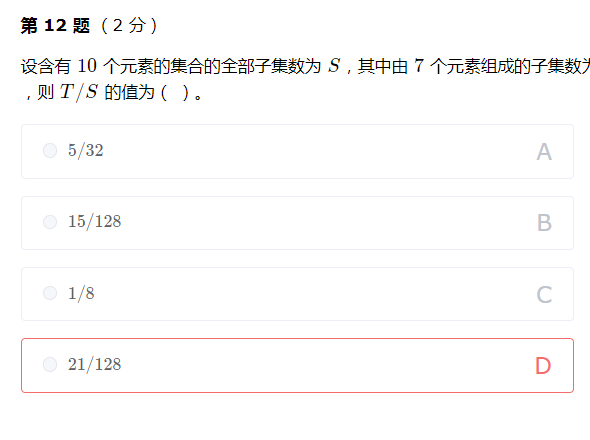
考察排列与组合基础知识。1010 个元素的集合的子集数有 2^{10}=10242
10
=1024 个,由 77 个元素组成的子集数有 C(10,7)= C(10,3)= 120C(10,7)=C(10,3)=120 种,故答案是 \dfrac{120} {1024} = \dfrac{15} {128}
1024
120
=
128
15
。
题目答案
B
题目解析
考察排列与组合基础知识。1010 个元素的集合的子集数有 2^{10}=10242
10
=1024 个,由 77 个元素组成的子集数有 C(10,7)= C(10,3)= 120C(10,7)=C(10,3)=120 种,故答案是 \dfrac{120} {1024} = \dfrac{15} {128}
1024
120
=
128
15
。

题目答案
B
题目解析
考察数论基础知识。1000010000 的质因子只有 22 和 55,能被 22 整除的数有 50005000 个,能被 55 整除的数有 20002000 个,但是即能被 22 整除,也能被 55 整除的数被算了两遍,即能被 1010 整除的 10001000 个数。
所以答案是 10000 - 5000 - 2000 + 1000 = 400010000−5000−2000+1000=4000。
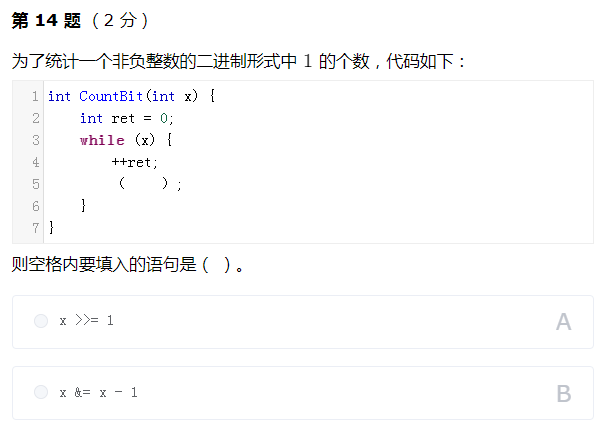
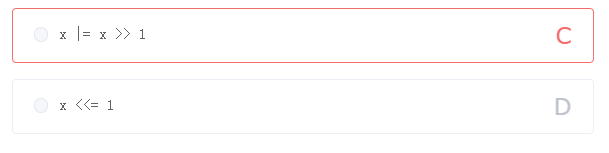
(最大公约数之和)下列程序想要求解整数 nn 的所有约数两两之间最大公约数的和对 1000710007 求余后的值,试补全程序。
举例来说,44 的所有约数是 1,2,41,2,4。11 和 22 的最大公约数为 11;22 和 44 的最大公约数为 22;11 和 44 的最大公约数为 11。于是答案为 1 + 2 + 1 = 41+2+1=4。
要求 getDivisor 函数的复杂度为 \mathcal{O}(\sqrt n)O(
n
),gcd 函数的复杂度为 \mathcal{O}(\log\ \max(a,b))O(log max(a,b))。
例如:
1
include [HTML_REMOVED]
2
using namespace std;
3
const int N = 110000, P = 10007;
4
int n;
5
int a[N], len;
6
int ans;
7
void getDivisor() {
8
len = 0;
9
for (int i = 1; ① <= n; i)
10
if (n % i == 0) {
11
a[len] = i;
12
if ( ② != i) a[len] = n / i;
13
}
14
}
15
}
16
int gcd(int a, int b) {
17
if (b == 0) {
18
③ ;
19
}
20
return gcd(b, ④ );
21
}
22
int main() {
23
cin >> n;
24
getDivisor();
25
ans = 0;
26
for (int i = 1; i <= len; i) {
27
for (int j = i + 1; j <= len; ++j) {
28
ans = ( ⑤ ) % P;
29
}
30
}
31
cout << ans << endl;
32
return 0;
33
}
题目答案
填空位置 ①:
i * i
填空位置 ②:
n / i
填空位置 ③:
return a
填空位置 ④:
a % b
填空位置 ⑤:
ans + gcd(a[i], a[j])
题目解析
枚举约数的时候,需要枚举到 n,所以第①空需要填 i * i,i * i <= n 就是枚举到 \sqrt n
n
。
如果 n % i == 0,ii 和 n / in/i 都是 nn 的约数,第 ② 空填 n / i 用于防止得到重复的约数。
第 ③④ 空位于辗转相除法求最大公约数函数里,分别填入 a 和 a % b。
第 ⑤ 空位于枚举约数,求两个约数的最大公约数并更新答案的地方,所以需要填上 ans + gcd(a[i], a[j])。
对于一个 11 到 nn 的排列 PP(即 11 到 nn 中每一个数在 PP 中出现了恰好一次),令 q_iq
i
为第 ii 个位置之后第一个比 P_iP
i
值更大的位置,如果不存在这样的位置,则 q_i=n+1q
i
=n+1。举例来说,如果 n = 5n=5 且 PP 为 1 5 4 2 315423,则 qq 为 2, 6, 6, 5, 62,6,6,5,6。
下列程序读入了排列 PP,使用双向链表求解了答案。试补全程序。
数据范围 1 \le n \le 10^51≤n≤10
5
。
1
include [HTML_REMOVED]
2
using namespace std;
3
const int N = 100010;
4
int n;
5
int L[N], R[N], a[N];
6
int main() {
7
cin >> n;
8
for (int i = 1; i <= n; i) {
9
int x;
10
cin >> x;
11
① ;
12
}
13
for (int i = 1; i <= n; i) {
14
R[i] = ② ;
15
L[i] = i - 1;
16
}
17
for (int i = 1; i <= n; i) {
18
L[ ③ ] = L[a[i]];
19
R[L[a[i]]] = R[ ④ ];
20
}
21
for (int i = 1; i <= n; i) {
22
cout << ⑤ << ” “;
23
}
24
cout << endl;
25
return 0;
26
}
题目答案
填空位置 ①:
a[x] = i
填空位置 ②:
i + 1
填空位置 ③:
R[a[i]]
填空位置 ④:
a[i]
填空位置 ⑤:
R[i]
题目解析
考察双向链表的基本操作。程序按照 xx 的值从 11 到 nn 枚举每个值,依次在双向链表中删除该点,删除的时候就可以知道该值左边最近比它大元素的位置和右边最近比它大元素的位置。
第 ① 空是 a 数组的初始化操作,标记每个值的位置,所以需要填 a[x] = i。
第 ② 空是双向链表指针的初始化操作,右指针指向右边相邻的元素,所以需要填 i + 1。
第 ③④ 空是双向链表的删除操作,当前元素右边元素的左指针需要指向左边元素,左边元素的右指针需要指向右边元素,所以分别填 R[a[i]] 和 a[i]。
最后需要输出答案,即 R[i] 的值,所以第 ⑤ 空需要填 R[i]。

