大话查并集

查并集，看名字，叫集合
看数据结构，其实是树
看实际用途，又跟图脱不开关系

所以，我们从实际出发，想想怎么用一个新的数据结构来处理图的连通性问题！

查并集和连通块

看图说话！！！

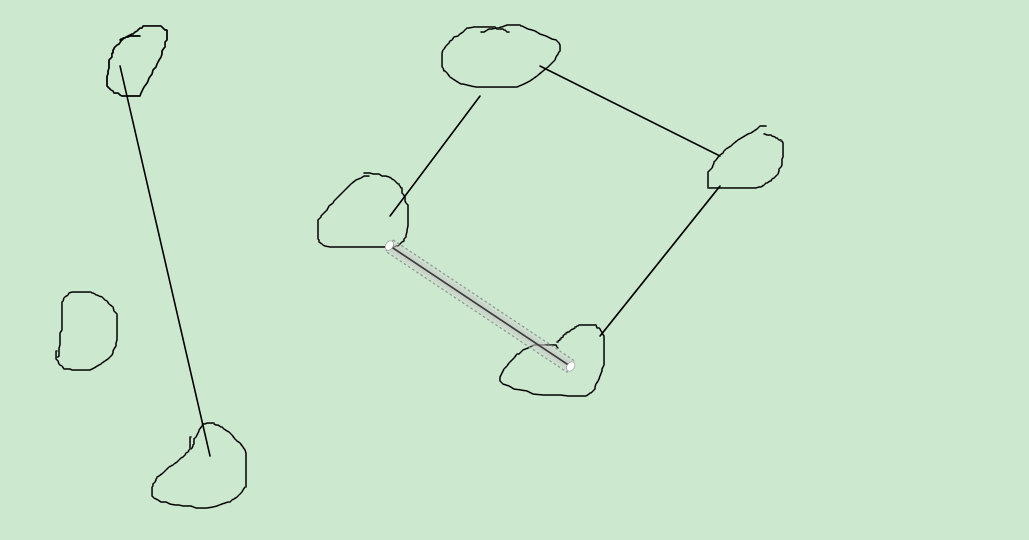
图也太难看了QAQ
不过这个图的连通性一目了然

现在，我们希望简化或者转化这个图，保持其连通性不变，从而提高查询效率

怎么办？就硬简化！
我们刚开始理解的是：不断删边，直到再删边就会导致连通性改变
像这样：

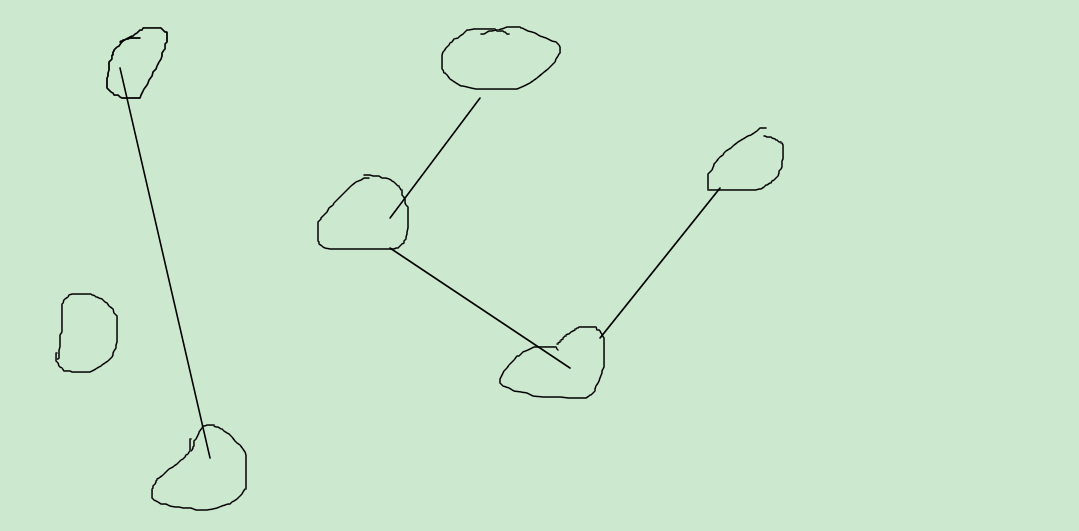
到现在，我们的图，就顺利的分为了很多的树！
为什么说是树呢，因为对于一个连通图，最少的边并保持连通的结构就是一种树啊（只不过没有严格规定层级）

那么到现在，我们的图已经简化不少了（这个例子里可能不明显）

但是我们还可以这样！

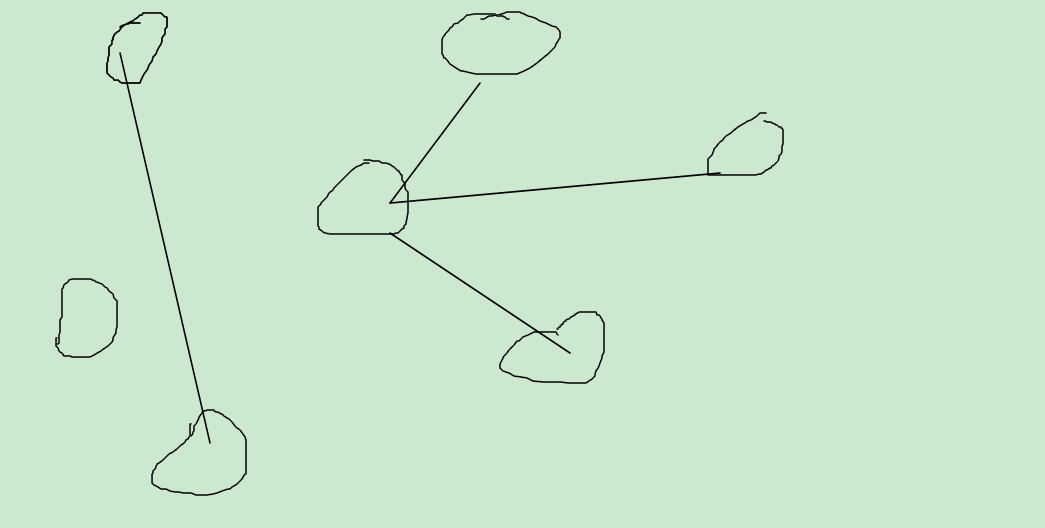
现在呢？
现在是一个层级为2的树！

我们再这个例子中需要考虑一个思想：
代言人思想（反正我是这么叫的）

我们先给上面的结点标号：

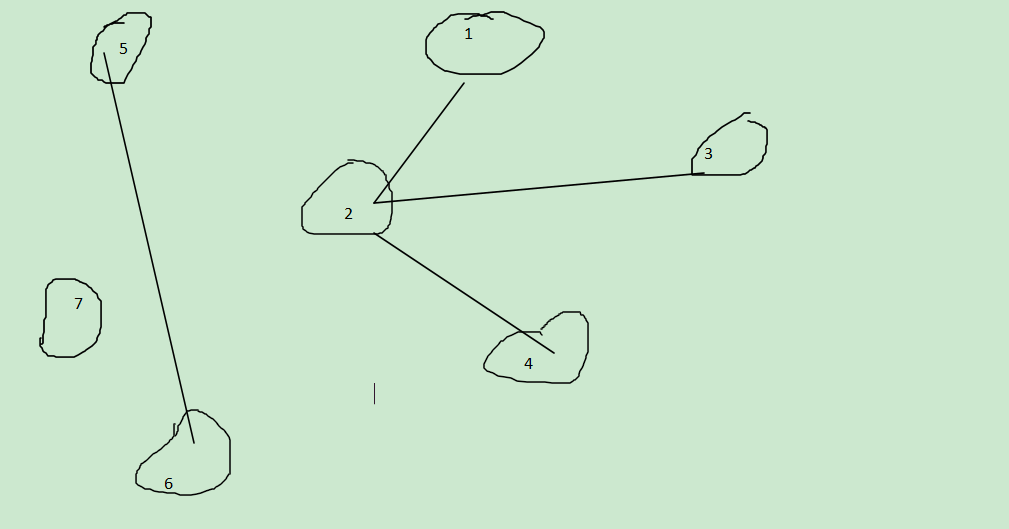
现在，我们这么理解：
1，2，3，4的代言人是2
5，6的代言人是5
7的代言人是7

所以，我现在判断两个点是否联通，只需要判断代言人就可以了！！

查并集模板思路

建立查并集
1，开始为独立集合，所有点的代言人为自己

2，给边，连接两个集合，默认以较小编号的作为代言人

就..就可以了呀

查询查并集
1，给一个点，找它代言人

如果它代言人不是自己，就获取它代言人的代言人
如果它代言人是自己，就返回自己

记得状态压缩，只需要把最高代言人作为自己代言人就好了！！

牙膏有限，日后更新qwq

更新：带权并查集

并查集进阶0.1 带权并查集

首先，你可以看一个例子来考虑一下解决：
NOI2001 食物链
题解链接

在这个例子里，我们很明显需要用到查并集，但是，一般的查并集好像并不足够解决该问题

这个问题的特点就在于，确定联系的两个点，他们之间的关系可以并不单一！

可能是同类，可能是食物，也可能是天敌

所以，我们需要一个权值来维护两个点之间的关系

但是，我们又不需要储存每一对关系，我们其实只需要知道每一点和公共祖先之间的关系，那么我们之间任何一对的关系其实也就可以确定好了！

而我们的加权查并集也就是这个意思，多加一个数组，保存该点和公共祖先的关系

当然，运用和变数远远不止这些，还需要我们在实战中继续摸索！

Over~