树状数组详解
我们都知道,二叉堆就是用数组来模拟的树结构,所以,数组是可以实现树结构的模拟的!
顾名思义,树状数组就是用数组模拟树的结构的一种方案,但是他又不像其他树一样,它是用来解决区间求和问题的!
和ST表很像,树状数组也是数组区间值快速查询的好东西!不同的是ST表是静态的,但是树状数组是可以中途修改的!(其实ST表也可以,但是不划算)
当然了,我更喜欢叫他动态前缀和
前情提要:需要先掌握位运算的知识!( 位运算)
树状数组怎么模拟的树?
先看一张图:
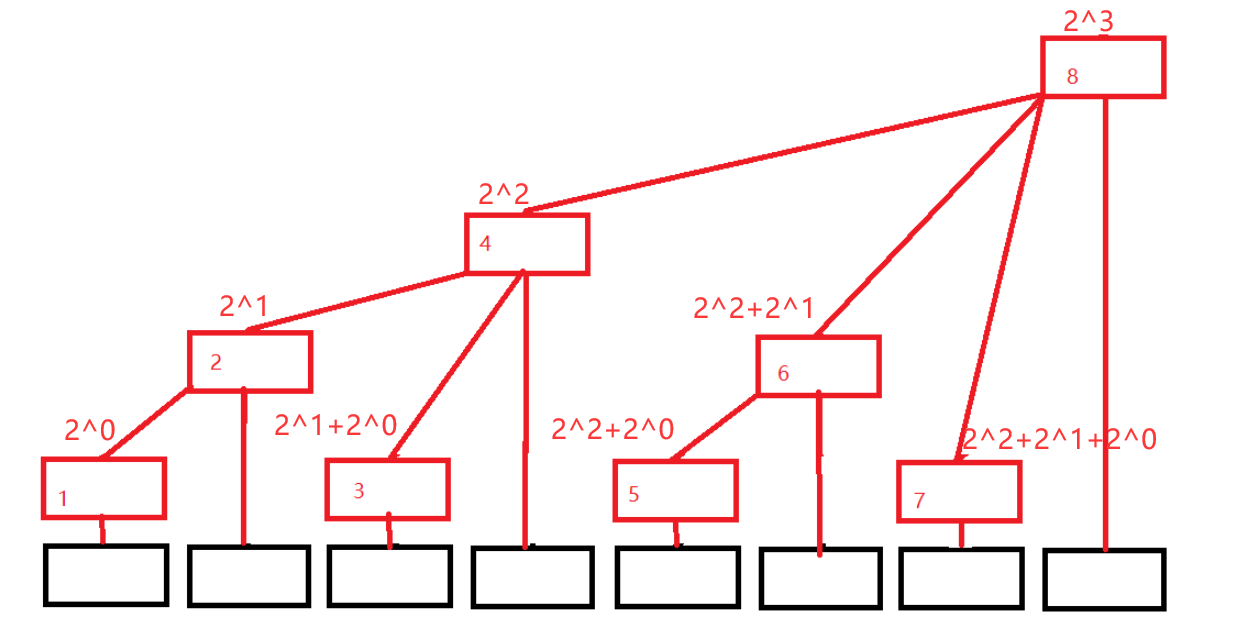
这树可不是随便建的!下面的黑色是原数组,红线连接表示上面的包含下面的(和的形式)
但是,光看这个图也看不出什么门道,所以,我们需要模拟一下我们查表的过程,来感受一下其中的奥妙
1,我们要查 1~6 的和
查询的时候,我们是这样的:
6的二进制:110
通过图,我们能看出来,查询的1~6和,只需要把t[6]+t[4]就可以了
但是,实际上,我们是这样查的:
t[110(2)]+t[100(2)]
也就是:先查一下6,再查一下6减去lowbit(最低位的1),得到4
看起来像巧合?我们再试一下7?
7 -》 111
t[111(2)]+t[110(2)]+t[100(2)]
也就是:t[7]+t[6]+t[4]
看图,是不是完全符合!
至此,规律已经出来了,就是对查询的数不断删去最低位的1,继续查询
为什么呢?
因为我们注意到这个图是这样储存的:
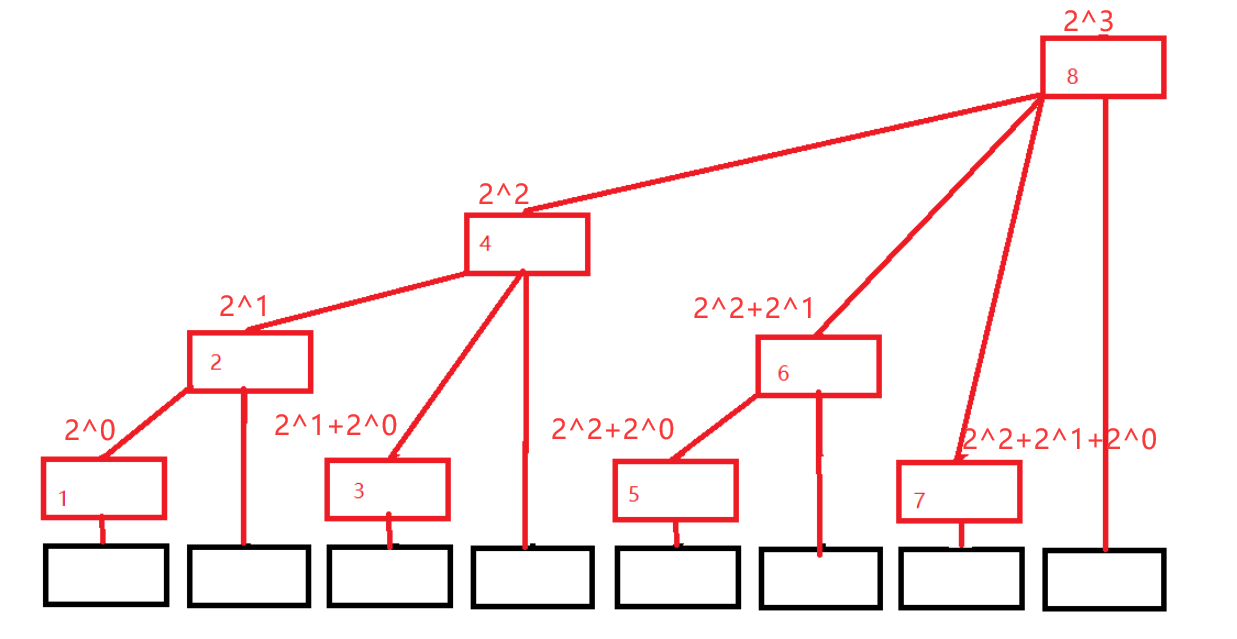
有没有一点ST表的意思了!至少你应该看出了倍增规律了!
仔细观察!
带2^0的(最低),只会存2^0个
带2^1的(最低),只会存2^1个
带2^2的(同上),只会存2^2个
…………
那么,对于一个数,都可以用二进制: 2^i1 + 2^i2 ……………… 2^lowbit 表示
那么,我们就可以分解出:
t[2^i1]+t[2^i1+2^i2]+………………t[2^i1+2^i2+…………2^lowbit]
而我们知道,t[2^i1+2^i2+…………2^lowbit]只包含了2^lowbit个数
所以累计下来,就不重复的包含了前 2^i1 + 2^i2 ……………… 2^lowbit个数!
这就是二进制!这就是倍增思想!
得到的结果就是前缀和!
对于原版前缀和,查询是O(1),修改是O(n)
但是对于树状数组,查询是O(logn),修改也是O(logn)
可以说是很平衡和高效的搭配了!
所以,理解了原理,接下来考虑实际的操作
1,建表
设w[i]为原数组,t[i]为树状数组
建表思路为,t[i]=w[i]+get_sum(i-lowbit(i),i-1)+w[i];
lowbit为查询最低位1的函数
get_sum为查表函数,也就是说,建表的过程,其实是一个递推的查表过程
因为,我们根据上面的可以知道,lowbit(i)是多少,那么t[i]就应该存放以i结尾的多少个元素的和,而前面的元素都已经准备好了,直接查表就可以了!
2,查表
查表思路为:
while(i!=0) sum+=t[i];i-=lowbit(i);
本来可以递归的,但是循环也很好理解,而且很高效
3,修改
比如,把w[i]加上p,(设一共n个数)
while(i<=n) t[i]+=p;i+=lowbit(i);
这里要解释一下,因为只有 大于i 且 范围包括i 的数需要加上p
而i+=lowbit(i)的结果,就相当于把i的最低位1往高位移
如果有连续多个1并不会导致出现问题,这是因为:
所有比他大的数中,只有这个数减去这个数的lowbit会小于等于他
具体例子可以参考7(二进制:111)
于是,建表,查表,修改都实现了,接下来开始打模板吧!
树状数组 模板题
#include <iostream>
#define LL long long
using namespace std;
LL w[500010],t[500010];
int n,T;
int lowbit(int i){
return i&(i^(i-1));
}
LL front_sum(int i){
LL sum=0;
while(i>0){sum+=t[i];i-=lowbit(i);}
return sum;
}
LL get_sum(int l,int r){
//cout << l << " " << r <<endl;
LL suml=front_sum(l),sumr=front_sum(r);
return sumr-suml;
}
void add(int i,int p){
while(i<=n){t[i]+=p;i+=lowbit(i);}
}
int main(){
cin >> n >> T;
//cout << lowbit(4) << " " << lowbit(8) << " "<<lowbit(256);
for(int i=1;i<=n;i++){
cin >> w[i];
t[i]=get_sum(i-lowbit(i),i-1)+w[i];
}
while(T--){
int a,b,c;
cin >> a >> b >> c;
if(a==1){
add(b,c);
}else if(a==2){
cout << get_sum(b-1,c) << endl;
}
}
return 0;
}

