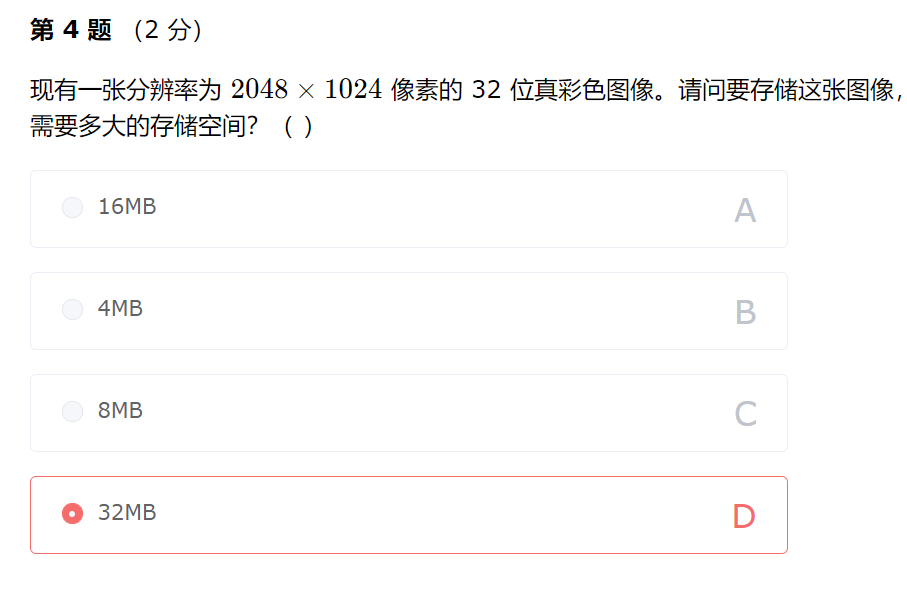
2048102412/8=8MB

解析：当数组L中的元素按照非递减顺序排列时，比较次数最少。此时，内层for循环执行n-1次，FLAG值始终为1。

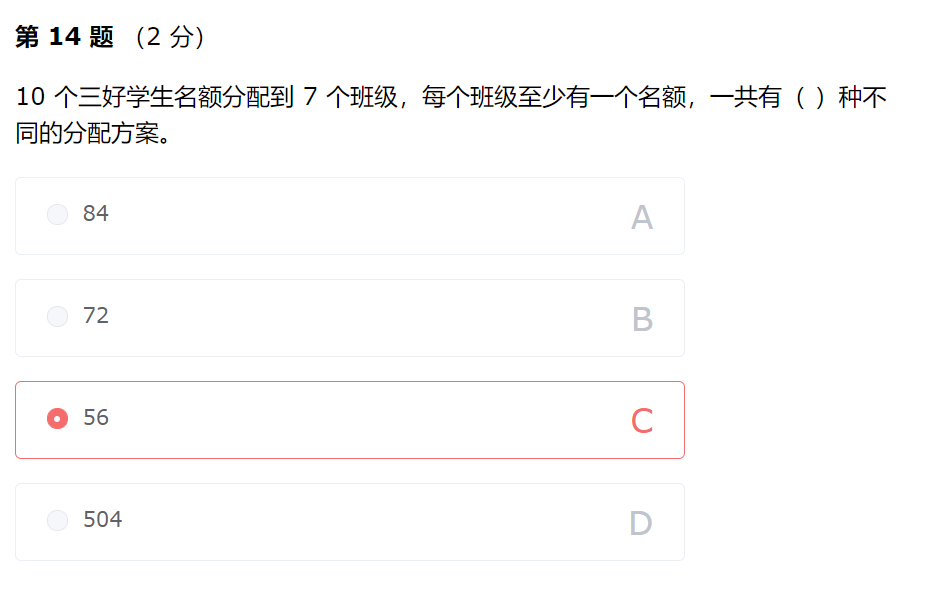
解析：每个班级至少有一个名额，那么还剩下3个名额，可以进行如下分类：
分给3个班，每班一个，从7个班中选3个班的方案有：C73=35C_7^3=35C73​=35分给2个班，一个班2个、一个班1个，从7班中选2个班的方案有：C 7 2 = 21C_7^2=21C72​=21；这两个班的名额交换过来又是一种方案，这样就有42种方案分给1个，从7个班中选1个班的方案有7种。利用加法原理，一共有84种方案
18题：

#include <cstdlib>
#include <iostream>
using namespace std;

char encoder[26] = {'C', 'S', 'P', 0};
char decoder[26];

string st;

int main() {
    int k = 0;
    for (int i = 0; i < 26; ++i)
        if (encoder[i] != 0) ++k;
    for (char x = 'A'; x <= 'Z'; ++x) {
        bool flag = true;
        for (int i = 0; i < 26; ++i)
            if (encoder[i] == x) {
                flag = false;
                break;
            }
        if (flag) {
            encoder[k] = x;
            ++k;
        }
    }
    for (int i = 0; i < 26; ++i)
        decoder[encoder[i] - 'A'] = i + 'A';
    cin >> st;
    for (int i = 0; i < st.length(); ++i)
        st[i] = decoder[st[i] - 'A'];
    cout << st;
    return 0;
}

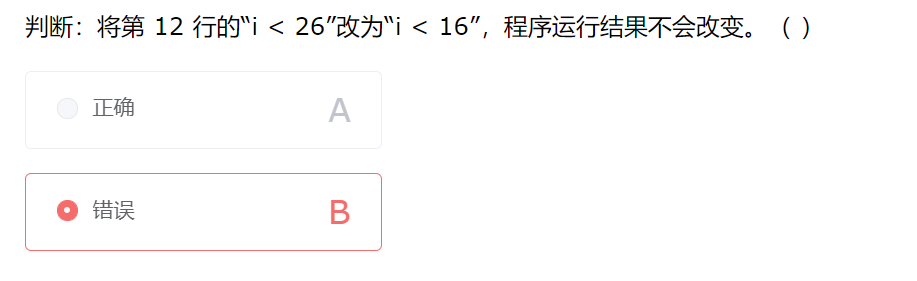
解析：encoder[]初始化为3个字符，所以第一段for循环改为i < 16，对程序结果不会有任何影响。
21题：

#include <cstdlib>
#include <iostream>
using namespace std;

char encoder[26] = {'C', 'S', 'P', 0};
char decoder[26];

string st;

int main() {
    int k = 0;
    for (int i = 0; i < 26; ++i)
        if (encoder[i] != 0) ++k;
    for (char x = 'A'; x <= 'Z'; ++x) {
        bool flag = true;
        for (int i = 0; i < 26; ++i)
            if (encoder[i] == x) {
                flag = false;
                break;
            }
        if (flag) {
            encoder[k] = x;
            ++k;
        }
    }
    for (int i = 0; i < 26; ++i)
        decoder[encoder[i] - 'A'] = i + 'A';
    cin >> st;
    for (int i = 0; i < st.length(); ++i)
        st[i] = decoder[st[i] - 'A'];
    cout << st;
    return 0;
}

解析：若输出CSPCSPCSPCSP，根据映射的对应关系，则输入字符串为PRNPRNPRNPRN，输入的字符串中既有 P 又有 R。
23和24题：

#include <iostream>
using namespace std;

long long n, ans;
int k, len;
long long d[1000000];

int main() {
    cin >> n >> k;
    d[0] = 0;
    len = 1;
    ans = 0;
    for (long long i = 0; i < n; ++i) {
        ++d[0];
        for (int j = 0; j + 1 < len; ++j) {
            if (d[j] == k) {
                d[j] = 0;
                d[j + 1] += 1;
                ++ans;
            }
        }
        if (d[len - 1] == k) {
            d[len - 1] = 0;
            d[len] = 1;
            ++len;
            ++ans;
        }
    }
    cout << ans << endl;
    return 0;

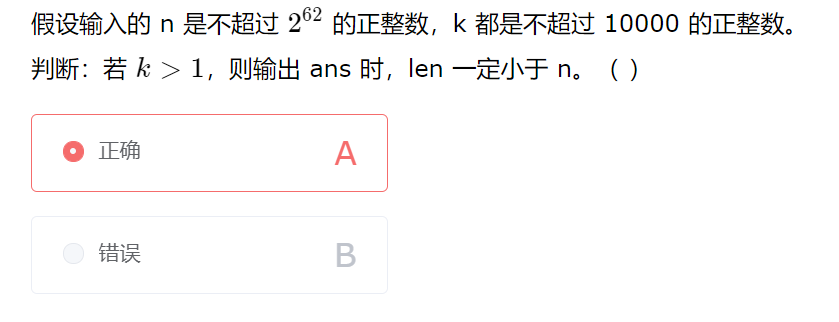
解析：举出一个反例即可，例如n = 1，k = 2时，将1转换为二进制的位数len = 1，此时len = n。

解析：除了k = 1的情况，任何数n转换为len位的k进制数后，k l e n > n k^{len} > nk len>n，例如8的转换二进制为(1000 ) 2 (1000)_2(1000) 2​ ，一共4位，而2 4 > 8 2^4>82 4>8。
27题：

#include <iostream>
using namespace std;

long long n, ans;
int k, len;
long long d[1000000];

int main() {
    cin >> n >> k;
    d[0] = 0;
    len = 1;
    ans = 0;
    for (long long i = 0; i < n; ++i) {
        ++d[0];
        for (int j = 0; j + 1 < len; ++j) {
            if (d[j] == k) {
                d[j] = 0;
                d[j + 1] += 1;
                ++ans;
            }
        }
        if (d[len - 1] == k) {
            d[len - 1] = 0;
            d[len] = 1;
            ++len;
            ++ans;
        }
    }
    cout << ans << endl;
    return 0;

解析：利用26题得到的结论，那么当k = 10 k=10k=10时：
累加到100 , 000 , 000 , 000 , 00累加到10 , 000 , 000 , 000，需要进位1 , 111 , 111 , 111 , 111次累加到2 , 000 , 000，需要进位2 × 111111 = 222 , 222 2 \times 111111=222,2222×111111=222,222次
累加到90 9090，需要进位9 × 1 = 9 9\times1=99×1=9次
总的进位次数a n s = 11 , 111 , 111 , 111 , 111 + 1 , 111 , 111 , 111 , 111 + 222 , 222 + 9 = 11 , 112 , 222 , 444 , 453 ans=11,111,111,111,111+1,111,111,111,111+222,222+9=11,112,222,444,453ans=11,111,111,111,111+1,111,111,111,111+222,222+9=11,112,222,444,453
32题：

#include <algorithm>
#include <iostream>
using namespace std;

int n;
int d[50][2];
int ans;

void dfs(int n, int sum) {
    if (n == 1) {
        ans = max(sum, ans);
        return;
    }
    for (int i = 1; i < n; ++i) {
        int a = d[i - 1][0], b = d[i - 1][1];
        int x = d[i][0], y = d[i][1];
        d[i - 1][0] = a + x;
        d[i - 1][1] = b + y;
        for (int j = i; j < n - 1; ++j)
            d[j][0] = d[j + 1][0], d[j][1] = d[j + 1][1];
        int s = a + x + abs(b - y);
        dfs(n - 1, sum + s);
        for (int j = n - 1; j > i; --j)
            d[j][0] = d[j - 1][0], d[j][1] = d[j - 1][1];
        d[i - 1][0] = a, d[i - 1][1] = b;
        d[i][0] = x, d[i][1] = y;
    }
}

int main() {
    cin >> n;
    for (int i = 0; i < n; ++i)
        cin >> d[i][0];
    for (int i = 0; i < n; ++i)
        cin >> d[i][1];
    ans = 0;
    dfs(n, 0);
    cout << ans << endl;
    return 0;
}

40、41、42题：

#include <iostream>

using namespace std;

const int MAXN = 5000;
int n, m;
struct segment { int a, b; } A[MAXN];

void sort() // 排序
{
    for (int i = 0; i < n; i++)
        for (int j = 1; j < n; j++)
            if (①)
            {
                segment t = A[j];
                ②
            }
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i++)
        cin >> A[i].a >> A[i].b;
    sort();
    int p = 1;
    for (int i = 1; i < n; i++)
        if (③)
            A[p++] = A[i];
    n = p;
    int ans = 0, r = 0;
    int q = 0;
    while (r < m)
    {
        while (④)
            q++;
        ⑤;
        ans++;
    }
    cout << ans << endl;
    return 0;
}

算法思想如下：

首先使用了冒泡排序的思想，将所有区间按照左端点从小到大排序。
去除所有被包含的区间，例如[3,10]、[4,9]，后面的区间被前面的区间包含了，不需要进行判断。
为覆盖区间[0,m]，将r设为 0，在区间数组中找到离r最近的、并且左端点<=r的区间q，使用区间q的右端点更新r，重复这个过程直到r>=m。。



空②，交换A[j]和A[j-1]，答案为A[j]=A[j-1];A[j-1]=t;
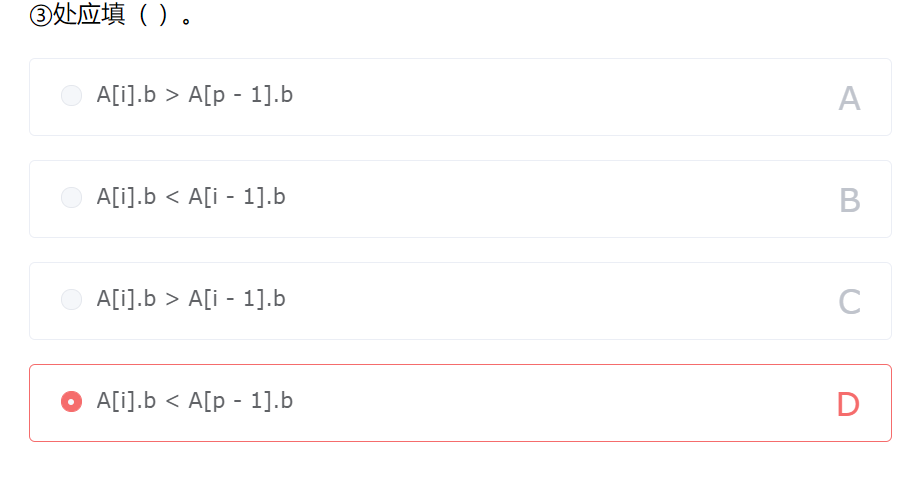
空③，去掉被包含的区间，只有当第i个和第p-1个区间不是包含关系时，将第i个区间放入第p个位置，答案为A[i].b>A[p-1].b
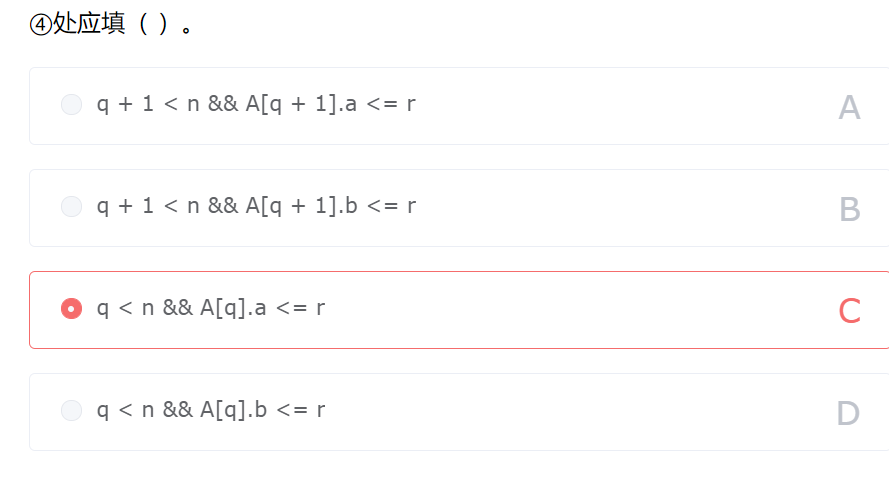
空④，找到r左边第一个区间q，答案为q + 1 < p && A[q + 1].a <= r