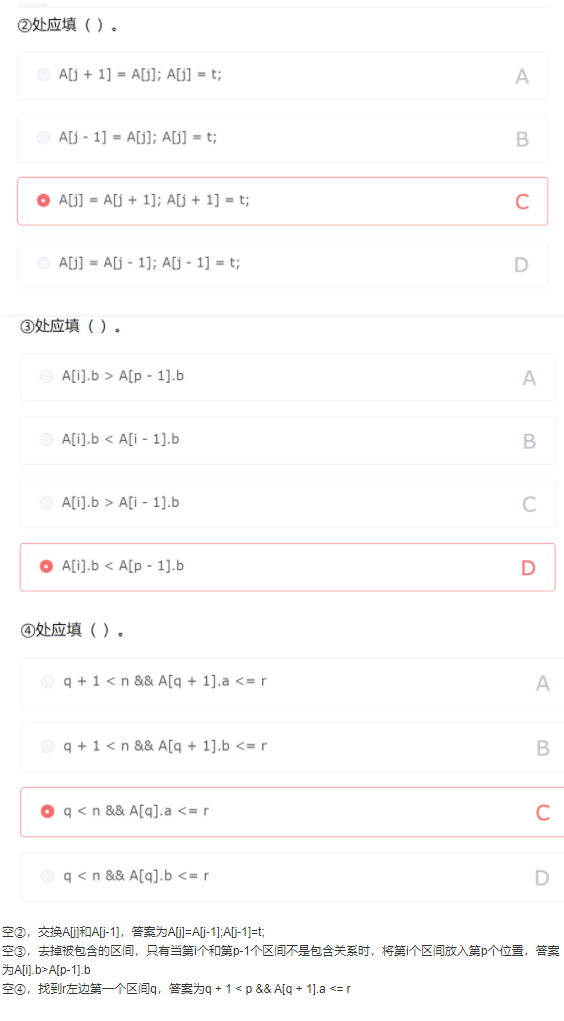
解析：当数组L中的元素按照非递减顺序排列时，比较次数最少。此时，内层for循环执行n-1次，FLAG值始终为1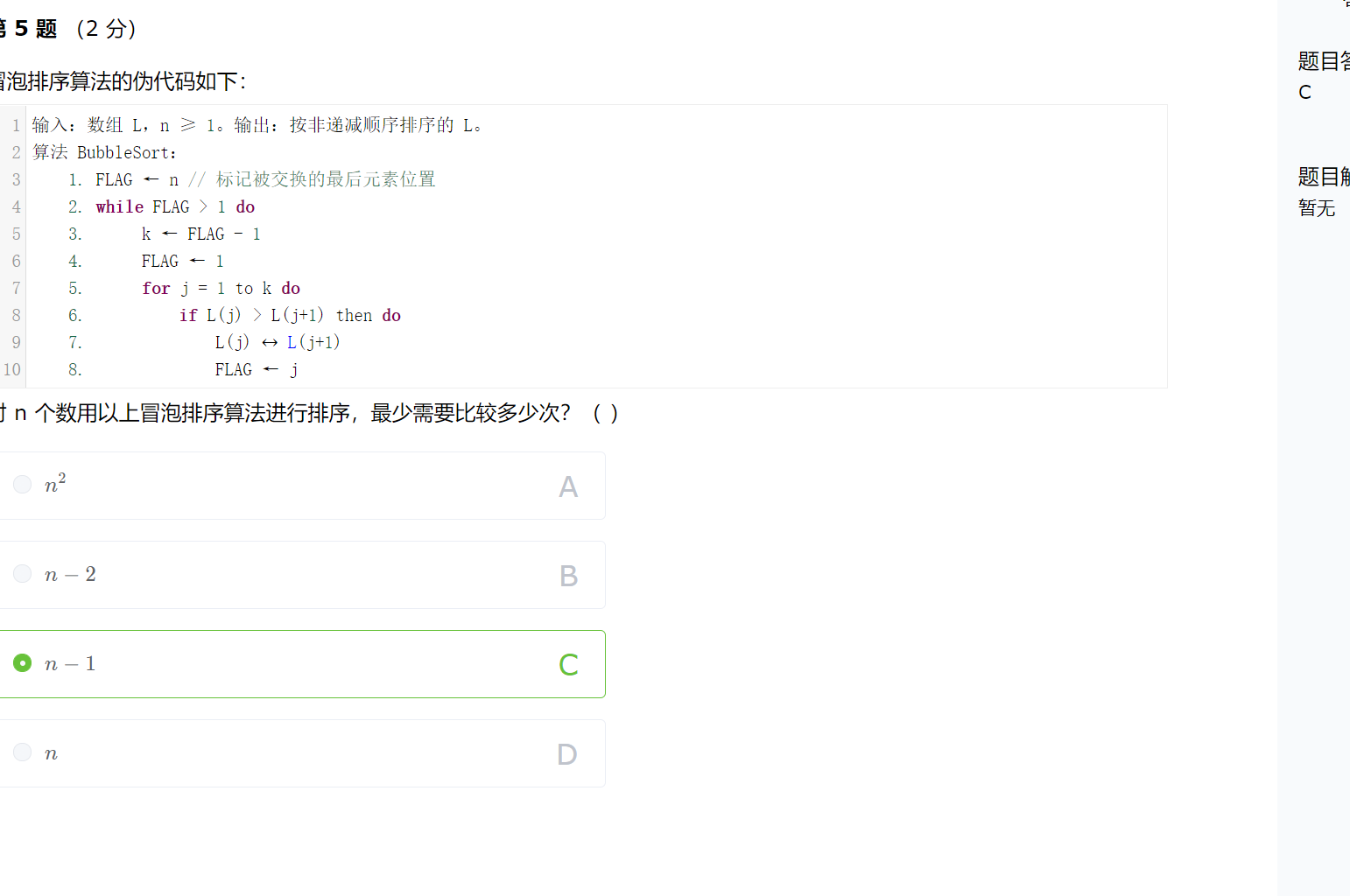 解析：每个班级至少有一个名额，那么还剩下3个名额，可以进行如下分类：
分给3个班，每班一个，从7个班中选3个班的方案有：C73=35C_7^3=35C73​=35分给2个班，一个班2个、一个班1个，从7班中选2个班的方案有：C 7 2 = 21C_7^2=21C72​=21；这两个班的名额交换过来又是一种方案，这样就有42种方案分给1个，从7个班中选1个班的方案有7种。利用加法原理，一共有84种方案

解析：encoder[]初始化为3个字符，所以第一段for循环改为i < 16，对程序结果不会有任何影响。
解析：除了k = 1的情况，任何数n转换为len位的k进制数后，k l e n > n k^{len} > nk len>n，例如8的转换二进制为(1000 ) 2 (1000)_2(1000) 2​ ，一共4位，而2 4 > 8 2^4>82 4>8。
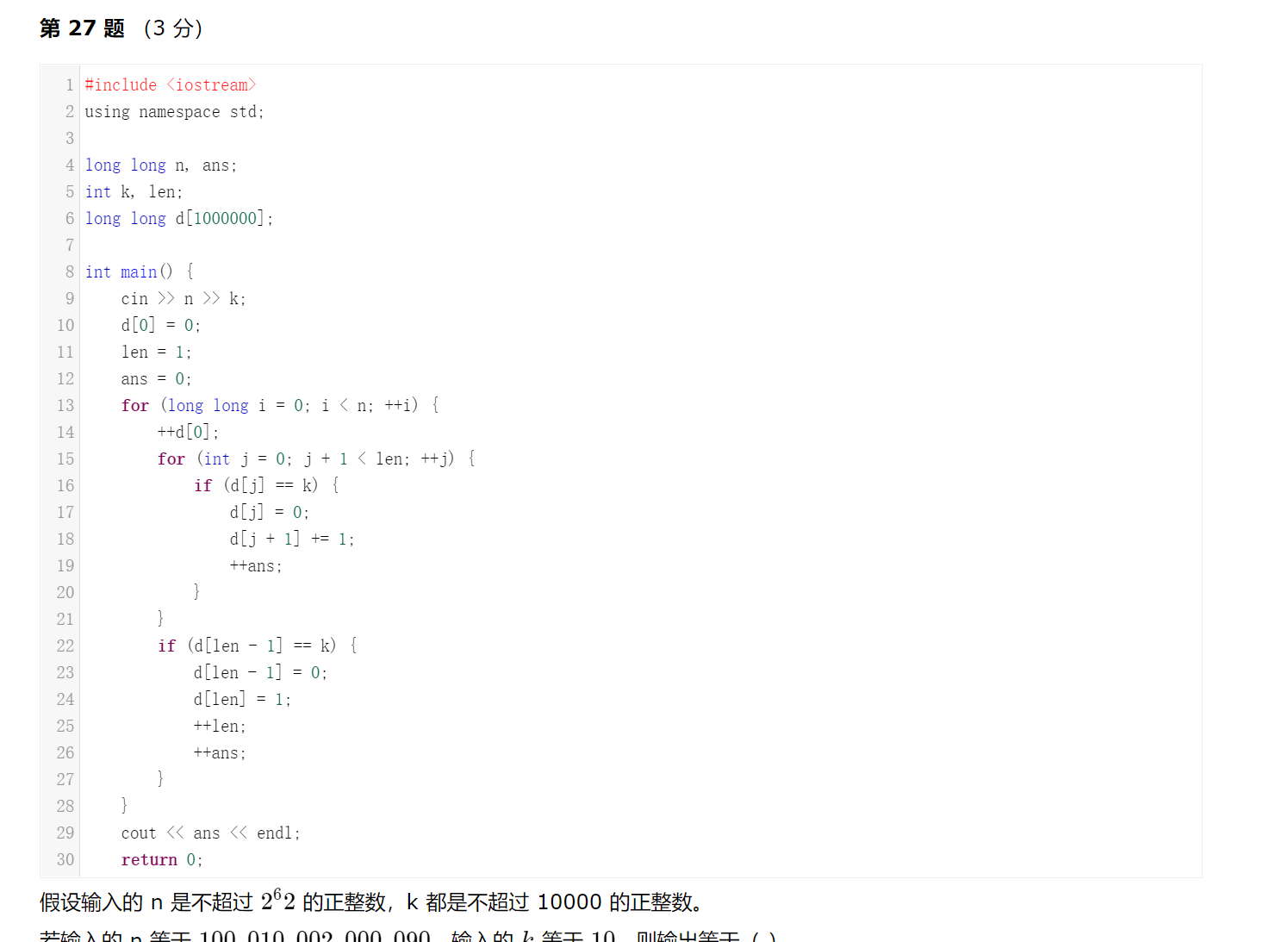
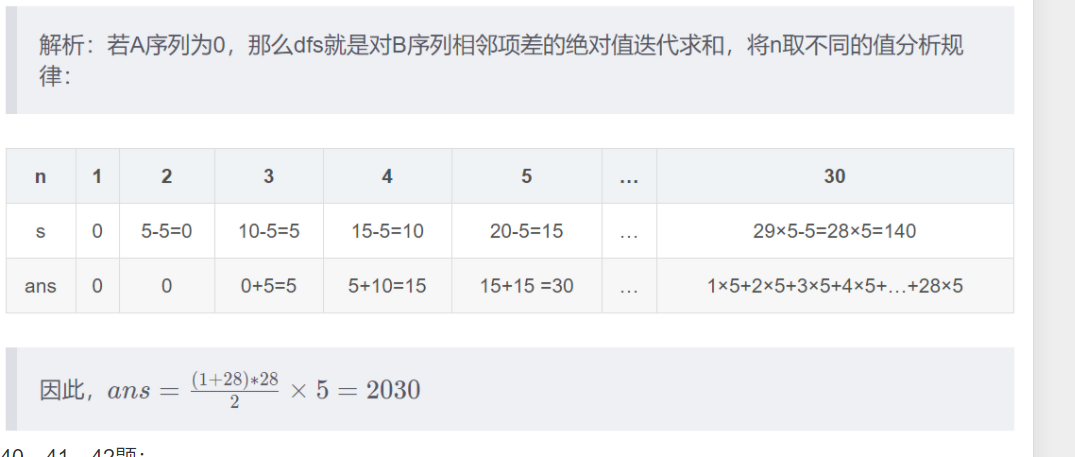
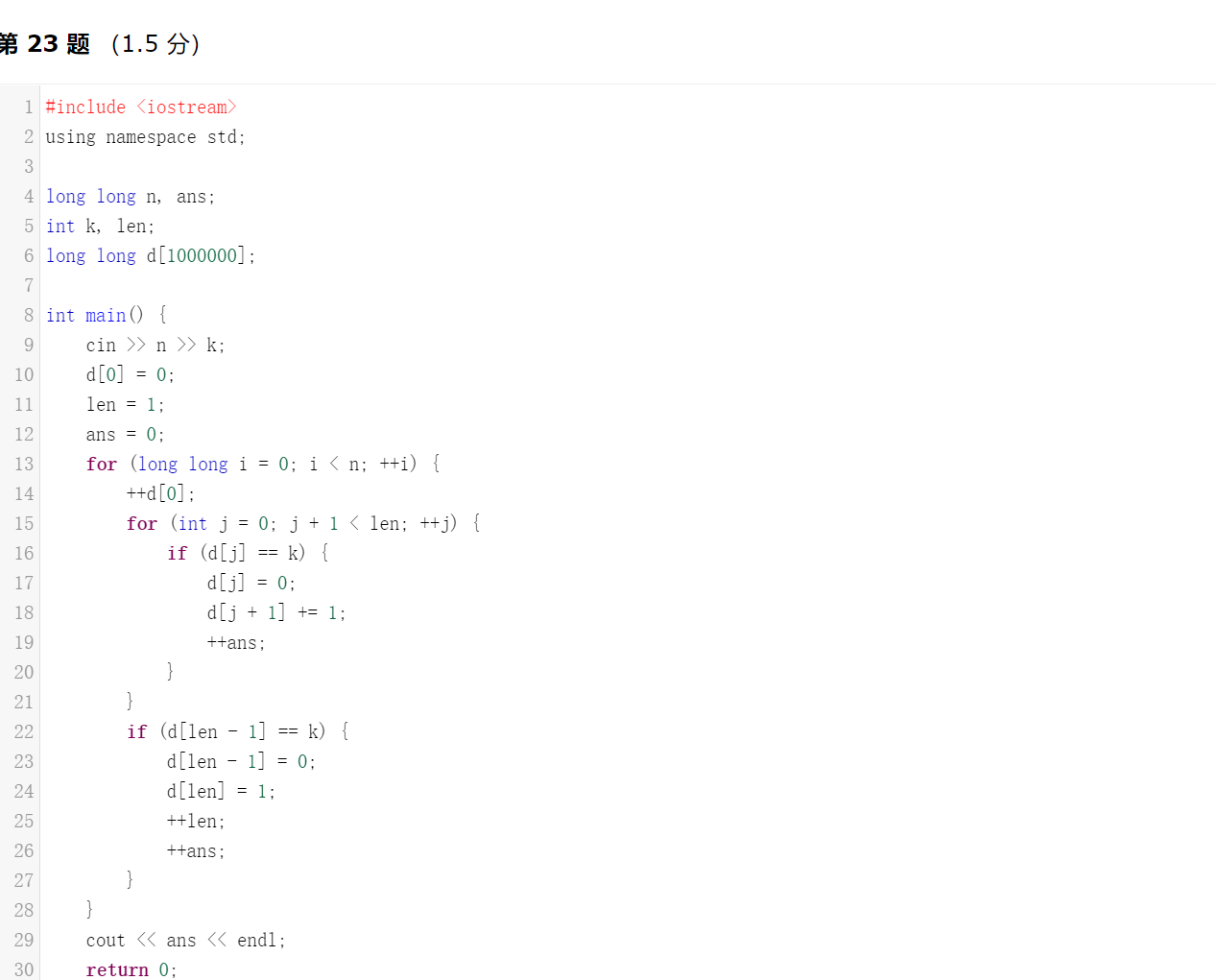解析：利用26题得到的结论，那么当k = 10 k=10k=10时：
累加到100 , 000 , 000 , 000 , 00累加到10 , 000 , 000 , 000，需要进位1 , 111 , 111 , 111 , 111次累加到2 , 000 , 000，需要进位2 × 111111 = 222 , 222 2 \times 111111=222,2222×111111=222,222次
累加到90 9090，需要进位9 × 1 = 9 9\times1=99×1=9次
总的进位次数a n s = 11 , 111 , 111 , 111 , 111 + 1 , 111 , 111 , 111 , 111 + 222 , 222 + 9 = 11 , 112 , 222 , 444 , 453 ans=11,111,111,111,111+1,111,111,111,111+222,222+9=11,112,222,444,453ans=11,111,111,111,111+1,111,111,111,111+222,222+9=11,112,222,444,453
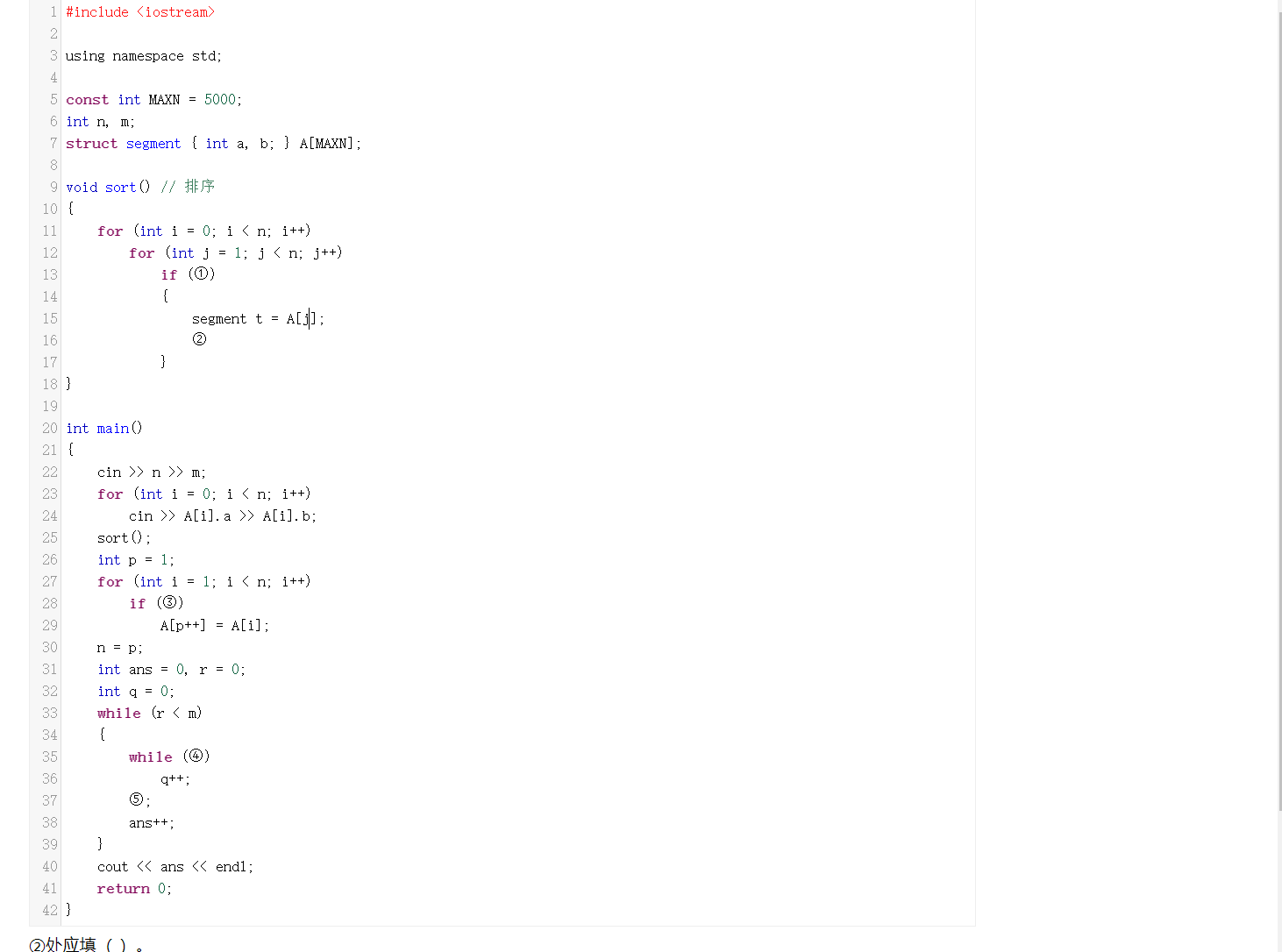
算法思想如下：

首先使用了冒泡排序的思想，将所有区间按照左端点从小到大排序。
去除所有被包含的区间，例如[3,10]、[4,9]，后面的区间被前面的区间包含了，不需要进行判断。
为覆盖区间[0,m]，将r设为 0，在区间数组中找到离r最近的、并且左端点<=r的区间q，使用区间q的右端点更新r，重复这个过程直到r>=m。。