Cut The Wire

两种情况
1. 偶数 从较大值向较小值连线 2 * n -> n
2. 奇数 从较小值向较大值转移 n -> 3 * n + 1\
于是
1. 偶数 只有大于 n / 2 小于等于 n 的才有线连接 (n + 1) / 2
2. 奇数 设 t 为有一条线经过 n 的最小值, 则 t < n 且3 * t + 1 > n , 得 (n - 1) / 3 < t < n , t 不能保证一定为奇数 要特判一下, 然后是从 t 到n 之间奇数个数个计算 (n - t + 1) / 2 , 但是发现当 n 为奇数是还是少一个 n 自己, 于是有 n % 2 == 1

#include <iostream>

using namespace std;

int main() {
    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        int t = (n + 2) / 3;
        if (t % 2 == 0) t++;
        cout << (n + 1) / 2 + (n - t + 1) / 2 + (n % 2 == 1) << endl;
    }
}

/*
2
12
60
*/

/*
10
50
*/

Power Sum

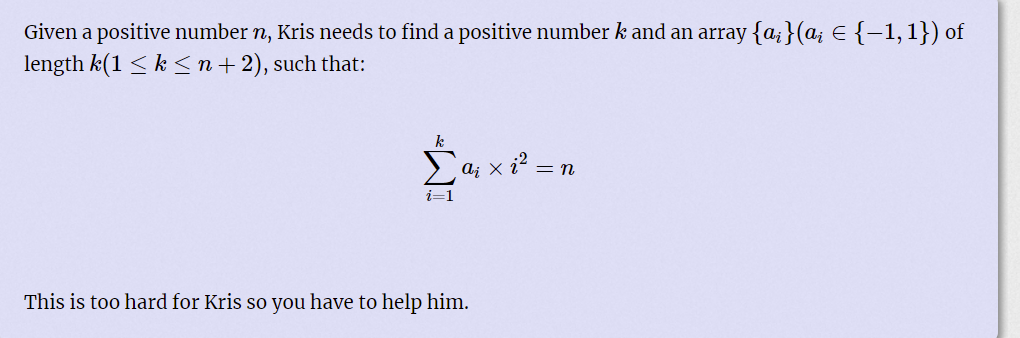
有一个小规律 任意四个连续的数字的平方 按照 1001 的方式计算 总可以的到一个 4
所以?
1. n % 4 == 0 直接输出n / 4 个1001
2. n % 4 == 1 多加一个”1”
3. n % 4 == 2 多加一个”0001”
4. n % 3 == 3 多加一个”01”

#include <iostream>

using namespace std;

int main(){
    int T;
    cin >> T;
    while(T --){
        int n;
        cin >> n;
        if(n % 4 == 0){
            cout << n << endl;
        }
        else if(n % 4 == 1){
            cout << 1 + n / 4 * 4 << endl;
            cout << "1";
        }
        else if(n % 4 == 2){
            cout << 4 + n / 4 * 4 << endl;
            cout << "0001";
        }
        else {
            cout << 2 + n / 4 * 4 << endl;
            cout << "01" << endl;
        }
        for(int i = 0; i < n / 4; i ++) cout << "1001" ; cout << endl;
    }
    return 0;
}

/*
2
1
5
*/

/*
1
1
2
11
*/

Command Sequence

问有多少个连续字串可以使人走回原地
开始想记录每一个位置每个字符的个数, 然后区间查值, 看看是不是上下左右分别相等, 但是时间要爆掉了
于是想如果某一段字符可以使人走回原地的话, 那么必然有上下左右的起点和终点的个数差值相等(有些差分的味道), 如果使用一个值来记录上下上++ 下–, 那么就是又回到这个值

#include <iostream>
#include <map>

using namespace std;
typedef long long LL;
typedef pair<LL, LL> PLL;

int n;
string str;
map<PLL, LL> mp;

int main(){
    int T;
    cin >> T;
    while(T --){
        mp.clear();

        cin >> n;
        cin >> str;

        LL a = 0, b = 0;
        mp[{ a, b }] ++; // { 0, 0 } 起点, 也算是一种
        for(auto i : str){
            if(i == 'U') a ++;
            else if(i == 'D') a --;
            else if(i == 'L') b ++;
            else b --;

            mp[{ a, b }] ++;
        }

        LL ans = 0;
        for(auto i : mp){
            LL t = i.second;
            ans += t * (t - 1) / 2;
        }
        cout << ans << endl;
    }
    return 0;
}

/*
1
6
URLLDR
*/

/*
2
*/

总结

HDU的服务器简直要把人弄崩溃, 5个小时罚坐罢了, 但不得不说 题目的质量还是很高的
三道签到题, 有不足之处还请指出