前缀和 Prefix-sum
很久之前写的笔记,现在搬过来
对于一个数组,如果我们想要求它在某一区间的所有数的和,我们需要把区间中的每个数加起来,这个时间复杂度是$O(n)$的。 如果我们想在$O(1)$的时间内求出/查询这个值,就可以借助前缀和。 前缀和,顾名思义,每个数存是在它前面所有数(前缀)的和,但是前缀和修改每个数的时间复杂度是$O(n)$的。
代码实现
在输入的时候进行累加即可,这个过程是递推的。
for (int i = 1; i <= n; i++){
cin >> num[i];
num[i] += num[i - 1];
}
求某个区间的值就是num[r]-num[l]。
例题
差分 Finite difference
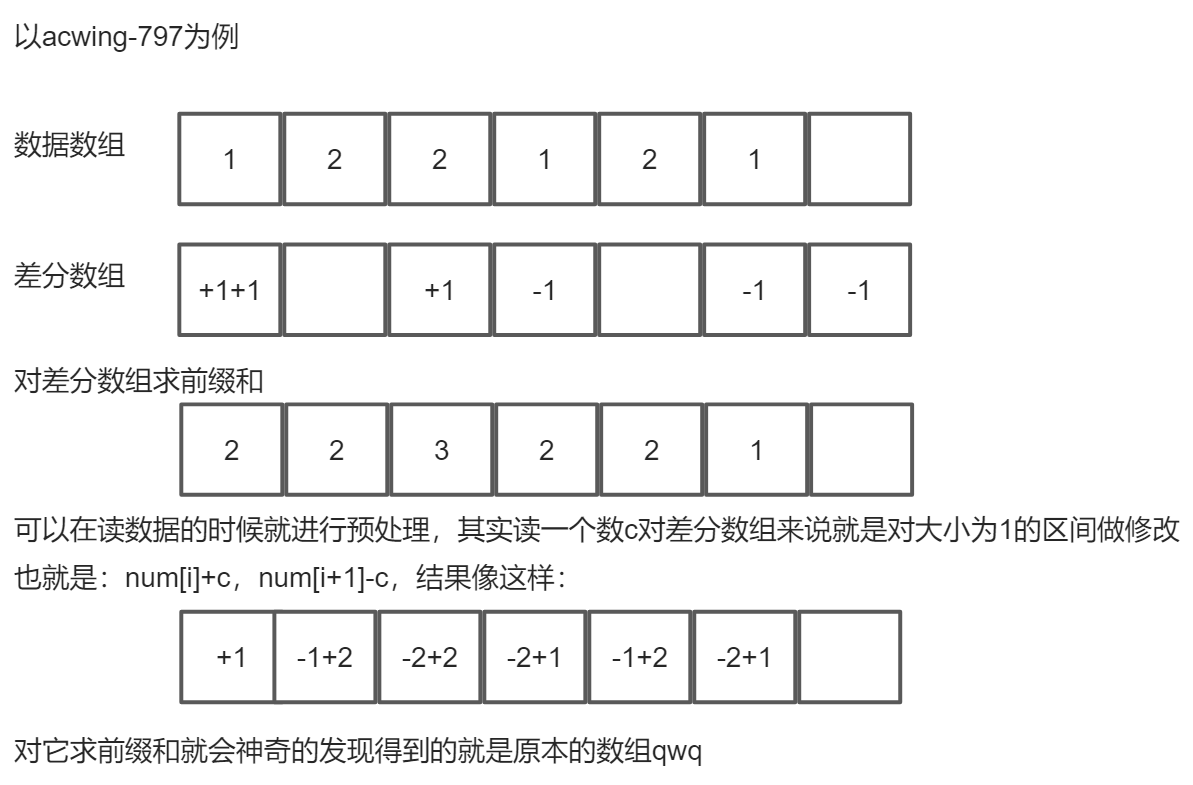
对一个数组,我们想构造一个数组使它的前缀和等于这个数组,这时候就要借助差分。 差分是前缀和的逆运算,对一个数组进行累加得到前缀和数组,对一个数组进行差分运算就得到差分数组,它们的关系大概是这样:

对一个数组的[l,r]区间进行修改,通常是加上或者减去一个数,不管是直接暴力修改原本的数组,还是修改前缀和,其时间复杂度都是$O(n)$的(前缀和更高,因为后面连带也要改),而使用差分可以在$O(1)$时间内实现。
差分的思路大概是这样的:对$num[l]$先加上要修改的数$c$,然后在对$num[r+1]$减去$c$,这样求对它前缀和的时候等价于$[l,r]$区间都加上了$c$,而$r+1$开始加$c$和减$c$抵消,后面的数就相当于不受影响,这样修改的时间成本就会降低到$O(1)$。
代码实现
//读入数据
for (int i = 1; i <= n; i++){
num[i] -= c;
cin >> c;
num[i] += c;
}
//区间修改
for (int i = 1; i <= m; i++){
cin >> l >> r >> c;
num[l] += c;
num[r + 1] -= c;
}
例题
拓展
前缀和和差分可以拓展到更高的维度,二维的前缀和就是前缀和矩阵,二维的差分就是差分矩阵,需要用到容斥原理,不过思想是类似的。


666