网络流的概念和定义整理

在图论中，网络流（英语：Network flow）是指在一个每条边都有容量（Capacity）的有向图分配流，使一条边的流量不会超过它的容量。

流网络 Flow Network

流网络是一种特殊的有向图。

一个网络可以表示成一个点集和边集的集合，即：

$$G=(V,E)$$

V表示点，流网络有两个特殊点，分别是源点和汇点。

E表示边，流网络中每条边都有一个权重c，被称之为容量（Capacity）。

源点 & 汇点

可以把流网络类比成一个由一条条河流组成的网络。

源点（Source）有无穷的的流量可以向外流出，汇点（Sink）有无穷的容量容纳流量。

净流

通过流网络的一条边的流量（净流）记为$f(u,v)$

可行流

可行流常用 $f$ 表示

在流网络中满足以下条件的网络流称为可行流

1. 容量限制（Capacity Constraints）:

   $\forall u,v\in V: 0\leq f(u,v)\leq c(u,v)$

2. 流守恒（Flow Conservation）:

   除了源点和汇点，所有点流出流量之和=流入流量之和

反之，如果只满足容量限制不满足流守恒则称之为伪流

可行流的流量

每秒从源点流出的净流量或者每秒从汇点流入的净流量就是该可行流的流量：

$$|f|=\sum_{s,v}{f(s,v)}-\sum_{v,s}{v,s}$$

式子也可以用汇点来表示。式子后半部分表示减去流回源点的流量。

最大流

最大流即为最大可行流

最大流的流量是所有可行流中最大的。

残留网络 Residual Network

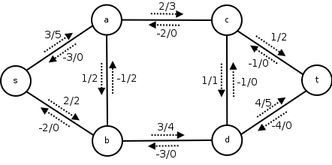
一个显示了流及容量的流网络及对应的残留网络

残留网络是由流网络 $G$ 和可行流 $f$ 决定的一个流网络，记为 $G_f$ ，它显示可用的容量的多少。

残留网络的点等于流网络 $G$ 的点：

$$V_f=V$$

残留网络的边等于原本的边和反向边之和

每条边的容量可以表示为：

$$c’(u,v)=\begin{cases} c(u,v)-f(u,v)\text{ if }(u,v)\in E\\ f(v,u)\text{ if } (v,u)\in E \end{cases}$$

分别表示剩余可用流量和反向流量（可以退回的流量）。

残留网络也是一个流网络，因此也有可行流的概念

定理：原网络的可行流 $f$ 加上 残留网络的一个可行流 $f’$ 也是原网络 $G$ 的一个可行流 ：

$$|f+f’|=|f|+|f’|$$

增广路径 Augmenting Path

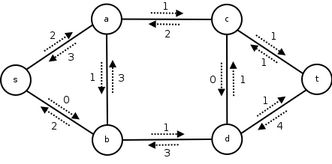
增广路是一条路径 ${\displaystyle (u_{1},u_{2},\cdots ,u_{k})}$，而 ${\displaystyle u_{1}=s}$ 、${\displaystyle u_{k}=t}$ 及 ${\displaystyle c_{f}(u_{i},u_{i+1})>0}$，这表示沿这条路径传送更多流是可能的。

一个流网络和残留网络的一条增广路

定理：一个可行流当且仅当剩余网络 ${\displaystyle G_{f}}$ 没有增广路时处于最大流。(这个后面会再提到)

割 Cut

割将一个流网络G分为两个图S和T，记为$[S,T]$，满足：

$$S\cup T=G$$

且：

$$S\cap T=\emptyset$$

源点满足 $s\in S$ ，汇点满足 $t\in T$

割的容量

所有从S指向T的有向边的容量之和为割的容量：

$$c(S,T)=\sum_{u\in S}\sum_{v\in T}c(u,v)$$

从T指向S的边则不被计算。

割的流量

类似割的容量，割的流量被定义为：

$$f(S,T)=\sum_{u\in S}\sum_{v\in T}f(u,v)-\sum_{u\in T}\sum_{v\in S}f(u,v)$$

可以注意到，容量和流量的定义不对称，容量只考虑正向边，流量考虑双向边。

最小割

容量最小的割即为最小割

割的性质

对于任意割，割的容量大于等于割的流量

$$\forall[S,T]\text{ }f(S,T)\leq c(S,T)$$

一个割只有一个容量，但可能有很多个流量（可行流），割的容量大于所有这个割的流量。

观察一下容量和流量的表达式，这条性质是很容易理解的。

对于任意一个可行流，和任意一个割，可行流的流量等于割的流量

$$|f|=f(S,T)$$

这个可以形象的理解，从源点流出的净流量一定全部流向了汇点，而割将源点和汇点分为了两部分，所以这些净流量一定流经了割。更加严谨的证明可以参考yxc的证明。

对于任意可行流，任意割，可行的流的流量一定小于割的容量

第一条性质再结合第二条性质，可以得到：

$$|f|= f(S,T)\le c(S,T)$$

也就是：

$$|f|\le c(S,T)$$

由于 $f$ 是任意的流，割是任意的割，因此最大流的流量一定小于等于最小割的容量。后面会证明，如果是这种情况的话，这里其实是取等号的。

最大流最小割定理

网络流的基石，核心概念

首先列出三个命题

对于一个流网络 $G$

1. $f$ 是最大流
2. $G_f$ 中不存在增广路
3. $\exists [S,T],|f|=c(S,T)$

最大流最小割定理证明了这三个命题是等价的。

$1\implies2$

首先证明1式可以推得2式，使用反证法

假定 $f$ 是 $G$ 的最大流，且残留网络 $G_f$ 存在增广路，那么 $G_f$ 中必定存在一个流量大于0的可行流 $f’$ 。

由定理 $|f+f’|=|f|+|f’|$ ，可得 $|f+f’|>f$ ，这与 $f$ 是最大流相矛盾，因此 $G_f$ 中不存在增广路，证毕。

$2\implies3$

尝试构造一个割，在残留网络 $G_f$ 中从源点s沿着正权路径遍历，能到达的所有点组成 $S$ ，其他点组成 $T$ 。这样就构造了一个合法的割。注意，这里的构造出的割是针对原图的割，而不是残留网络。

在 $S$ 中任取一点 $x$ ，在 $T$ 中任取一点 $y$ ，可以证明 $f(x,y)=c(x,y)$ ，且 $f(y,x)=0$ ：

1. 假定 $f(x,y) < c(x,y)$ ，那么在残留网络中就存在一条 $c(x,y)-f(x,y)>0$ 的边，按照构造割时候的方法，$y$ 点应该在 $S$ 中，这与假设矛盾，所以 $f(x,y)=c(x,y)$ 。
2. 假定 $f(y,x)\not= 0$ ，由于残留网络会建反向边，所以在残留网络中，必定存在 $f’(x,y)>0$ ，同样按照构造割的方法，$y$ 点应该在 $S$ 中，这与假设矛盾，所以 $f(y,x)=0$ 。

前面提到，对于任意一个可行流，和任意一个割，可行流的流量等于割的流量：

$$|f|=f(S,T)$$

所以：

$$|f|=f(S,T)=\sum_{u\in S}\sum_{v\in T}{f(u,v)}-\sum_{u\in S}\sum_{v\in T}{f(v,u)}$$

又因为在构造的割中，$f(x,y)=c(x,y),f(y,x)=0$ ，所以：

$$|f|=f(S,T)=\sum_{u\in S}\sum_{v\in T}{c(u,v)}=c(S,T)$$

$3\implies1$

这里要证明的是3式中的 $f$ 就是最大流。

不妨记最大流为$F$

首先 $|F|\ge |f|$ ，又因为 $|f|=c(S,T)\ge |F|$ ，所以 $|F|=|f|$ ，证毕。

这个式子还可以继续推导，记最小割为 $[S,T]_{min}$

$$c[S,T]_{min}\leq c[S,T]=|f|=|F|$$

又因为最小割的容量大于等于最大流的流量

$$c[S,T]_{min}\geq |F|$$

所以最小割的容量等于最大流的流量

$$c[S,T]=|F|$$

和起来就是：

$$1\implies2\implies3\implies1$$

所以这三个命题是等价的，这就是最大流最小割定理。

Ref

wikipedia:网络流

oi-wiki:网络流简介

yxc:网络流的基本概念