C 杨辉三角

链接：https://ac.nowcoder.com/acm/contest/11213/C
来源：牛客网

小F对杨辉三角颇有研究，他把杨辉三角第$n$行的数提出来，从左到右分别为$a[0],a[1],…,a[n−1]$。
现在他想知道$\sum_{i=0}^{n-1}i^2 * a[i]$的值是多少，答案对$99824353$取模。

输入描述

输入一个正整数$n$，$n\leq 10^{18}$

输出描述

输出题目中式子的值，答案对$99824353$取模。

输入样例

3

输出样例

6

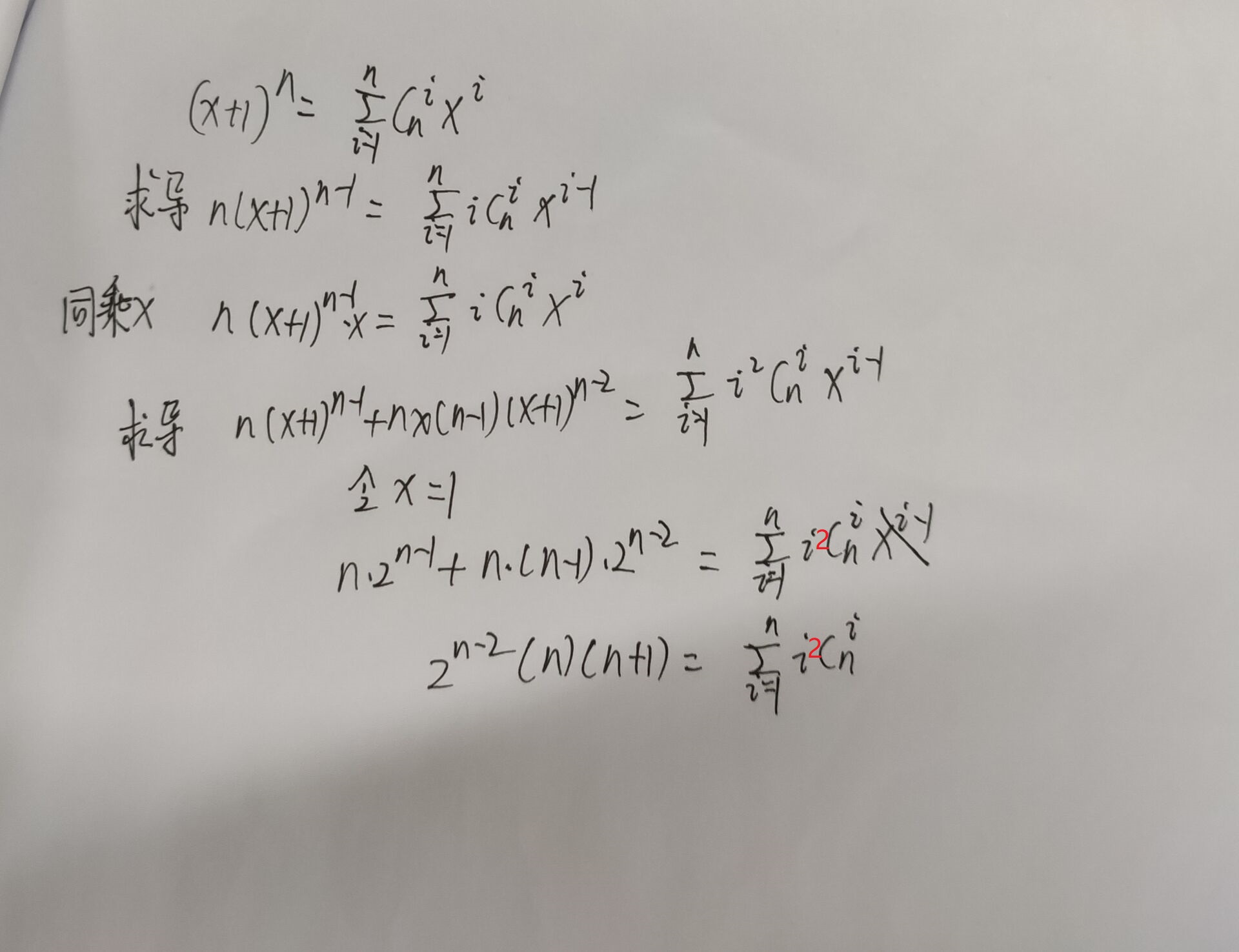
代码

#include<iostream>

using namespace std;

typedef long long LL;

const int mod = 99824353;

LL qmi(LL a, LL b){
    if(b < 0) return 1;
    LL res = 1;
    while(b){
        if(b & 1) res = (LL)res * a % mod;
        a = (LL)a * a % mod;
        b >>= 1;
    }

    return res % mod;
}
int main(){
    LL n;
    cin >> n;
    if(n == 2) {
        cout << 1 << endl;
        return 0;
    }
    n --;
    cout << n % mod * (n + 1) % mod * qmi(2, n - 2) % mod << endl;
}

B最短串

链接：https://ac.nowcoder.com/acm/contest/11213/B
来源：牛客网

题目描述
给定$2$个由小写字母和问号组成的字符串$a$与$b$，问号代表你想要的任何字符。
请你找出最短的字符串$s$，要求$s$包含$a$和$b$两个字符串，你只需要输出$s$的长度即可。
输入描述:
第一行一个字符串$a$，$|a| \leq 5000$

第二行一个字符串$b$，$|b| \leq 5000$

输出描述:
输出最短字符串$s$的长度。

示例1
输入

abc
?de

输出

5

思路

双指针, 对a串和b串分别作为主串跑一遍双指针, 若满足if(a[i] == '?' || b[j] == '?' || a[i] == b[j]); 则另一个串即子串指针可以后移一位，注意当j=0时需要再判断一次，并且若子串匹配成功,及时break

代码

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 5010;
string a, b;

bool check(int i, int j){
    if(a[i] == '?' || b[j] == '?' || a[i] == b[j]) return true;
    return false;
}

int main(){
    cin >> a >> b;

    int j = 0;
    for(int i = 0; i < a.size(); i ++){
        if(j == (int)b.size()) break;
        if(check(i, j)) j ++;
        else {
            j = 0;
            if(check(i, j)) j ++;
        }
    }

    int ans1 = a.size() + (b.size() - j);

    j = 0;
    for(int i = 0; i < b.size(); i ++){
        if(j == (int)a.size()) break;
        if(check(j, i)) j ++;
        else {
            j = 0;
            if(check(j, i)) j ++;
        }
    }

    int ans2 = b.size() + (a.size() - j);

    int ans = min(ans1, ans2);

    cout << ans << endl;


    return 0;
}

H卷王之王

链接：https://ac.nowcoder.com/acm/contest/11213/H
来源：牛客网

题目描述
牛卷风是养蛊大学著名的小镇做题家，每天早上6点半起床，凌晨2点半睡觉，除了一日三餐，其他时间均用来学习，因此考试从未低于90分，人送外号“养蛊大学不眠传说”。

你从四处打听到，牛卷风如此之强的原因在于他有一套练习计算能力的秘诀，该秘诀如下：首先给出$n$个数字，第$i$个数字为$a[i]$。接下来进行mm次操作，每次操作给出一个数字xx，练习者在心中将所有值小于等于$x$的数字都加$x$。当进行完这$m$次操作后，练习者再按顺序给出这$n$个数字。

话不多说，你立马着手练习。首先你让朋友给出一开始的$n$个数字和$m$次操作的$x$，请你给出进行完$m$次操作后的$n$个数字。

输入描述:
第一行两个正整数$n$, $m$, $n \leq 10^5$, $m \leq 10^5$
。

第二行$n$个非负整数$a[i]$, $a[i] \leq 10^9$

接下来$m$行，每行一个非负整数$x$, $x \leq 10^9$

输出描述:

输出进行完$m$次操作后的$n$个数字。

输入

5 2
1 2 3 4 5
2
3

输出

6 4 6 4 5

思路

卷吧，都给我卷。
线段树维护区间最小值, 区间最小值要大于 $x$, 直接返回。

#include<bits/stdc++.h>
#define rep(i, a, b) for(int i = a; i <= b; i ++)
#define pre(i, a, b) for(int i = a; i >= b; i --)
#define N 100005
using namespace std;
struct Node{
    int l, r;
    int val;
}tr[N << 2];
int n, m, a[N];
#define L tr[u].l
#define R tr[u].r
#define ls (u << 1)
#define rs (ls | 1)
#define S tr[u].val

void build(int u, int l, int r){
    L = l, R = r;
    if(l == r) S = a[l];
    else {
        int mid = l + r >> 1;
        build(ls, l, mid);
        build(rs, mid + 1, r);
        //pushup
        S = min(tr[ls].val, tr[rs].val);
    }
}

void modify(int u, int val){
    if(S > val) return;
    if(L == R) S += val;
    else {
        if(tr[ls].val <= val) modify(ls, val);
        if(tr[rs].val <= val) modify(rs, val);
        S = min(tr[ls].val, tr[rs].val);
    }
}

void query(int u){
    if(L == R) printf("%d ", S);
    else query(ls), query(rs);
}

int main(){
    scanf("%d%d", &n, &m);
    rep(i, 1, n) scanf("%d", &a[i]);
    build(1, 1, n);
    while(m --){
        int x;
        scanf("%d", &x);
        if(x == 0) continue;
        modify(1, x);
    }

    query(1);

    return 0;
}

哥三好

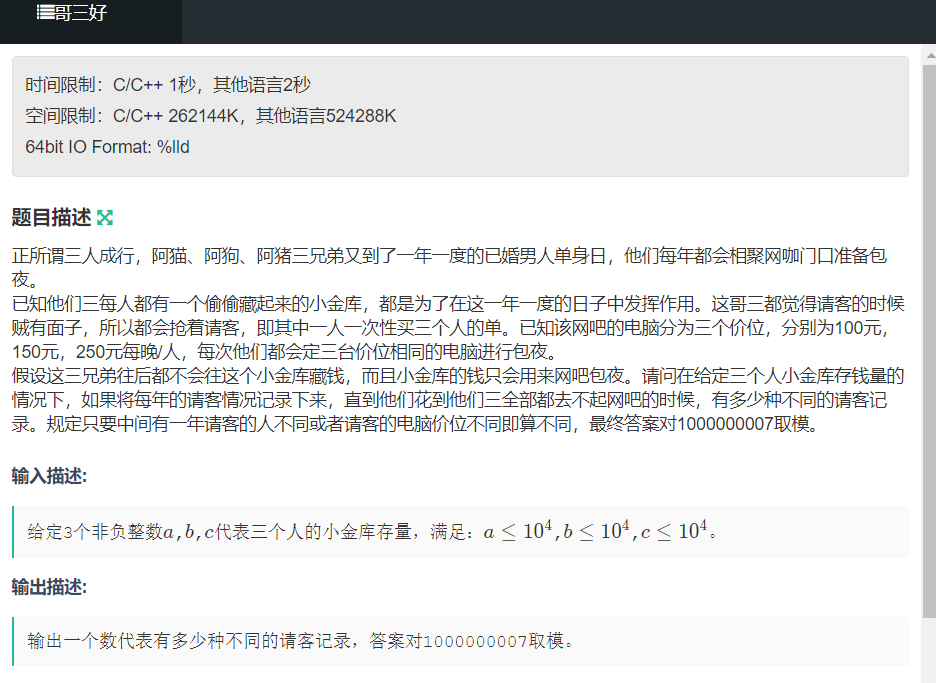
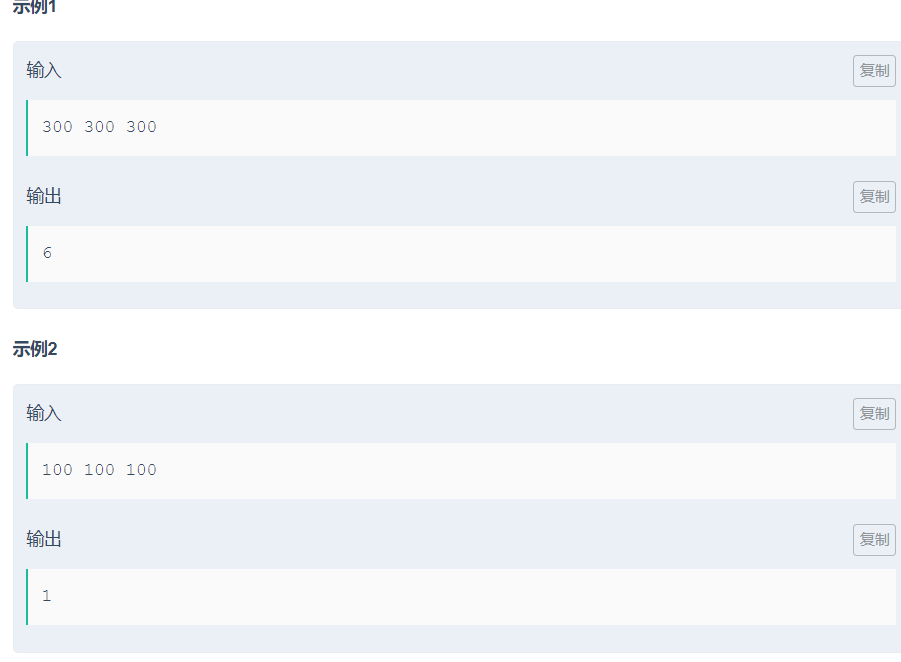
解法：

朴素三维DP, 可发现每个人花钱都是300 || 450 || 750， 则一开始都可以除150， 降低开销。
状态表示: f[i][j][k] a花i元，b花j元，c花k元，的方案种数
答案: f[a][b][c]
状态转移:
6种情况, a人 花 2, 3, 5 b人 花 2, 3, 5, c人花2， 3，5

#include<iostream>

using namespace std;

const int N = 110, mod = 1000000007;
int f[N][N][N];
int main(){
    int a, b, c;
    cin >> a >> b >> c;
    a /= 150;
    b /= 150;
    c /= 150;

    for(int i = 0; i <= 1; i ++)
        for(int j = 0; j <= 1; j ++)
            for(int k = 0; k <= 1; k ++)
                f[i][j][k] = 1;

    for(int i = 0; i <= a; i ++)
        for(int j = 0; j <= b; j ++)
            for(int k = 0; k <= c; k ++){
                if(i >= 2) f[i][j][k] = (f[i][j][k] + f[i - 2][j][k]) % mod;
                if(i >= 3) f[i][j][k] = (f[i][j][k] + f[i - 3][j][k]) % mod;
                if(i >= 5) f[i][j][k] = (f[i][j][k] + f[i - 5][j][k]) % mod;

                if(j >= 2) f[i][j][k] = (f[i][j][k] + f[i][j - 2][k]) % mod;
                if(j >= 3) f[i][j][k] = (f[i][j][k] + f[i][j - 3][k]) % mod;
                if(j >= 5) f[i][j][k] = (f[i][j][k] + f[i][j - 5][k]) % mod;

                if(k >= 2) f[i][j][k] = (f[i][j][k] + f[i][j][k - 2]) % mod;
                if(k >= 3) f[i][j][k] = (f[i][j][k] + f[i][j][k - 3]) % mod;
                if(k >= 5) f[i][j][k] = (f[i][j][k] + f[i][j][k - 5]) % mod;
            }

    cout << f[a][b][c] % mod<< endl;

    return 0;
}