7-1 Good in C(20分)
When your interviewer asks you to write “Hello World” using C, can you do as the following figure shows?

Input Specification:
Each input file contains one test case. For each case, the first part gives the 26 capital English letters A-Z, each in a 7×5 matrix of C’s and .’s. Then a sentence is given in a line, ended by a return. The sentence is formed by several words (no more than 10 continuous capital English letters each), and the words are separated by any characters other than capital English letters.
It is guaranteed that there is at least one word given.
Output Specification:
For each word, print the matrix form of each of its letters in a line, and the letters must be separated by exactly one column of space. There must be no extra space at the beginning or the end of the word.
Between two adjacent words, there must be a single empty line to separate them. There must be no extra line at the beginning or the end of the output.
Sample Input:
..C..
.C.C.
C...C
CCCCC
C...C
C...C
C...C
CCCC.
C...C
C...C
CCCC.
C...C
C...C
CCCC.
.CCC.
C...C
C....
C....
C....
C...C
.CCC.
CCCC.
C...C
C...C
C...C
C...C
C...C
CCCC.
CCCCC
C....
C....
CCCC.
C....
C....
CCCCC
CCCCC
C....
C....
CCCC.
C....
C....
C....
CCCC.
C...C
C....
C.CCC
C...C
C...C
CCCC.
C...C
C...C
C...C
CCCCC
C...C
C...C
C...C
CCCCC
..C..
..C..
..C..
..C..
..C..
CCCCC
CCCCC
....C
....C
....C
....C
C...C
.CCC.
C...C
C..C.
C.C..
CC...
C.C..
C..C.
C...C
C....
C....
C....
C....
C....
C....
CCCCC
C...C
C...C
CC.CC
C.C.C
C...C
C...C
C...C
C...C
C...C
CC..C
C.C.C
C..CC
C...C
C...C
.CCC.
C...C
C...C
C...C
C...C
C...C
.CCC.
CCCC.
C...C
C...C
CCCC.
C....
C....
C....
.CCC.
C...C
C...C
C...C
C.C.C
C..CC
.CCC.
CCCC.
C...C
CCCC.
CC...
C.C..
C..C.
C...C
.CCC.
C...C
C....
.CCC.
....C
C...C
.CCC.
CCCCC
..C..
..C..
..C..
..C..
..C..
..C..
C...C
C...C
C...C
C...C
C...C
C...C
.CCC.
C...C
C...C
C...C
C...C
C...C
.C.C.
..C..
C...C
C...C
C...C
C.C.C
CC.CC
C...C
C...C
C...C
C...C
.C.C.
..C..
.C.C.
C...C
C...C
C...C
C...C
.C.C.
..C..
..C..
..C..
..C..
CCCCC
....C
...C.
..C..
.C...
C....
CCCCC
HELLO~WORLD!
Sample Output:
C...C CCCCC C.... C.... .CCC.
C...C C.... C.... C.... C...C
C...C C.... C.... C.... C...C
CCCCC CCCC. C.... C.... C...C
C...C C.... C.... C.... C...C
C...C C.... C.... C.... C...C
C...C CCCCC CCCCC CCCCC .CCC.
C...C .CCC. CCCC. C.... CCCC.
C...C C...C C...C C.... C...C
C...C C...C CCCC. C.... C...C
C.C.C C...C CC... C.... C...C
CC.CC C...C C.C.. C.... C...C
C...C C...C C..C. C.... C...C
C...C .CCC. C...C CCCCC CCCC.
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 26, W = 5, H = 7;
char s[N][H][W];
int main()
{
for (int x = 0; x < N; x ++ )
for (int i = 0; i < H; i ++ )
for (int j = 0; j < W; j ++ )
cin >> s[x][i][j];
getchar();
string str;
getline(cin, str);
bool flag = false;
for (int i = 0, j = 0; i < str.size(); i = j + 1, flag = true)
{
while((str[i] < 'A' || str[i] > 'Z') && i < str.size())
i++;
j = i;
while((str[j] >= 'A' && str[j] <= 'Z') && j < str.size())
j++;
if(i >= j)
break;
char all[H][24 * W];
for(int x = 0; x < H; x++)
for (int y = 0; y < 24 * W; y ++ )
all[x][y] = ' ';
for(int x = i, cnt = 0; x < j; x++, cnt++)
for (int uh = 0 ; uh < H; uh ++ )
for(int uw = 0; uw < W; uw++)
all[uh][5 * cnt + uw + cnt] = s[str[x] - 'A'][uh][uw];
if(flag)
cout << endl;
for(int x = 0; x < H; x++)
{
for(int y = 0; y < (5 + 1) * (j - i) - 1; y++)
cout << (char)all[x][y];
cout << endl;
}
}
return 0;
}
7-2 Block Reversing (25 分)
Given a singly linked list L. Let us consider every K nodes as a block (if there are less than K nodes at the end of the list, the rest of the nodes are still considered as a block). Your job is to reverse all the blocks in L. For example, given L as 1→2→3→4→5→6→7→8 and K as 3, your output must be 7→8→4→5→6→1→2→3.
Input Specification:
Each input file contains one test case. For each case, the first line contains the address of the first node, a positive N (≤$10^5$) which is the total number of nodes, and a positive K (≤N) which is the size of a block. The address of a node is a 5-digit nonnegative integer, and NULL is represented by −1.
Then N lines follow, each describes a node in the format:
Address Data Next
where Address is the position of the node, Data is an integer, and Next is the position of the next node.
Output Specification:
For each case, output the resulting ordered linked list. Each node occupies a line, and is printed in the same format as in the input.
Sample Input:
00100 8 3
71120 7 88666
00000 4 99999
00100 1 12309
68237 6 71120
33218 3 00000
99999 5 68237
88666 8 -1
12309 2 33218
Sample Output:
71120 7 88666
88666 8 00000
00000 4 99999
99999 5 68237
68237 6 00100
00100 1 12309
12309 2 33218
33218 3 -1
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 1e5 + 10;
int head, m, k;
int datas[N], ne[N];
int main()
{
cin >> head >> m >> k;
while (m -- )
{
int address, d, next;
cin >> address >> d >> next;
datas[address] = d, ne[address] = next;
}
vector<int> list;
while(head != -1)
{
list.push_back(head);
head = ne[head];
}
for (int i = 0, j = k; i < list.size(); i ++ , i = j, j = min(j + k, (int)list.size()))
reverse(list.begin() + i, list.begin() + j);
reverse(list.begin(), list.end());
for (int i = 0; i + 1 < list.size(); i ++ )
printf("%05d %d %05d\n", list[i], datas[list[i]], list[i + 1]);
printf("%05d %d -1\n", list.back(), datas[list.back()]);
return 0;
}
7-3 Summit (25 分)
A summit (峰会) is a meeting of heads of state or government. Arranging the rest areas for the summit is not a simple job. The ideal arrangement of one area is to invite those heads so that everyone is a direct friend of everyone.
Now given a set of tentative arrangements, your job is to tell the organizers whether or not each area is all set.
Input Specification:
Each input file contains one test case. For each case, the first line gives two positive integers N (≤ 200), the number of heads in the summit, and M, the number of friendship relations. Then M lines follow, each gives a pair of indices of the heads who are friends to each other. The heads are indexed from 1 to N.
Then there is another positive integer K (≤ 100), and K lines of tentative arrangement of rest areas follow, each first gives a positive number L (≤ N), then followed by a sequence of L distinct indices of the heads. All the numbers in a line are separated by a space.
Output Specification:
For each of the K areas, print in a line your advice in the following format:
if in this area everyone is a direct friend of everyone, and no friend is missing (that is, no one else is a direct friend of everyone in this area), print Area X is OK..
if in this area everyone is a direct friend of everyone, yet there are some other heads who may also be invited without breaking the ideal arrangement, print Area X may invite more people, such as H. where H is the smallest index of the head who may be invited.
if in this area the arrangement is not an ideal one, then print Area X needs help. so the host can provide some special service to help the heads get to know each other.
Here X is the index of an area, starting from 1 to K.
Sample Input:
8 10
5 6
7 8
6 4
3 6
4 5
2 3
8 2
2 7
5 3
3 4
6
4 5 4 3 6
3 2 8 7
2 2 3
1 1
2 4 6
3 3 2 1
Sample Output:
Area 1 is OK.
Area 2 is OK.
Area 3 is OK.
Area 4 is OK.
Area 5 may invite more people, such as 3.
Area 6 needs help.
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <unordered_set>
using namespace std;
const int N = 210;
int n, m, k;
bool G[N][N];
unordered_set<int> s;
bool judge(vector<int> a)
{
for (int i = 0; i < a.size(); i ++ )
for (int j = 0; j < a.size(); j ++ )
if(!G[a[i]][a[j]])
return false;
return true;
}
int cal(vector<int> a)
{
if(!judge(a))
return -1;
s.clear();
for (int i = 0; i < n; i ++ )
s.insert(a[i]);
for(int i = 1; i <= n; i++)
{
if(s.count(i))
continue;
a.push_back(i);
if(judge(a))
return i;
a.pop_back();
}
return 0;
}
void init()
{
for (int i = 0; i < N; i ++ )
G[i][i] = true;
}
int main()
{
init();
cin >> n >> m;
while (m -- )
{
int a, b;
cin >> a >> b;
G[a][b] = G[b][a] = true;
}
cin >> k;
for (int i = 1; i <= k; i ++ )
{
int m, x;
cin >> m;
vector<int> a;
while(m--)
{
cin >> x;
a.push_back(x);
}
int res = cal(a);
if(res == 0)
printf("Area %d is OK.\n", i);
else if(res > 0)
printf("Area %d may invite more people, such as %d.\n", i, res);
else
printf("Area %d needs help.\n", i);
}
return 0;
}
7-4 Cartesian Tree (30 分)
A Cartesian tree is a binary tree constructed from a sequence of distinct numbers. The tree is heap-ordered, and an inorder traversal returns the original sequence. For example, given the sequence { 8, 15, 3, 4, 1, 5, 12, 10, 18, 6 }, the min-heap Cartesian tree is shown by the figure.
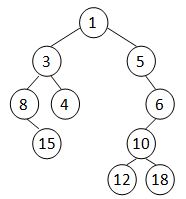
Your job is to output the level-order traversal sequence of the min-heap Cartesian tree.
Input Specification:
Each input file contains one test case. Each case starts from giving a positive integer N (≤30), and then N distinct numbers in the next line, separated by a space. All the numbers are in the range of int.
Output Specification:
For each test case, print in a line the level-order traversal sequence of the min-heap Cartesian tree. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the beginning or the end of the line.
Sample Input:
10
8 15 3 4 1 5 12 10 18 6
Sample Output:
1 3 5 8 4 6 15 10 12 18
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
using namespace std;
const int N = 36;
int n;
int a[N], q[N];
unordered_map<int, int> l, r;
int get_min(int il, int ir)
{
int m = il;
for (int i = il; i <= ir; i ++ )
if(a[m] > a[i])
m = i;
return m;
}
int build(int i, int j)
{
if(i == j)
return a[i];
int k = get_min(i, j);
int root = a[k];
if(i < k)
l[root] = build(i, k - 1);
if(k < j)
r[root] = build(k + 1, j);
return root;
}
void bfs(int root)
{
int hh = 0, rr = 0;
q[rr++] = root;
while(hh < rr)
{
int t = q[hh++];
if(l.count(t))
q[rr++] = l[t];
if(r.count(t))
q[rr++] = r[t];
}
for (int i = 0; i < n; i ++ )
cout << q[i] << (i == n - 1 ? '\n' : ' ');
}
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ )
cin >> a[i];
int root = build(0, n - 1);
bfs(root);
return 0;
}

