关键路径及代码实现
一. 问题描述
概念
-
一项工程计划可以被看成一个有向图,图中的顶点表示事件,边代表活动,边上的权值代表完成这项活动需要的时间,这样的有向图称为AOE网。
-
表示实际工程计划的AOE网应该是无环的,在正常情况下存在唯一的开始顶点(源点)和唯一的完成顶点(汇点)。
-
AOE网中的某些活动可以并行进行,完成工程的最短时间是从开始顶点到完成顶点的最长路径长度。路径长度最长的路径为关键路径。关键路径上所有活动都叫做关键活动。我们只有减少关键路径上活动用时才能加快工程的进度。
-
我们的问题就是输出所有关键路径上的顶点。
一个例子
- 如下图,求出下图的关键路径。
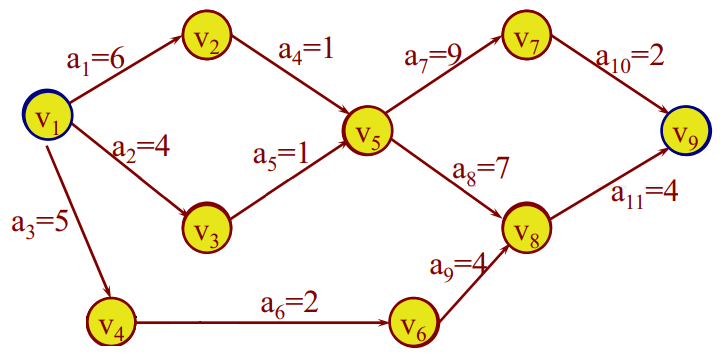
-
如下图,青色代表的两条路径就是关键路径。只有减少这两条路径上活动用时才能加快工程进度。
-
关键路径为:
1->2->5->8->9和1->2->5->7->9。
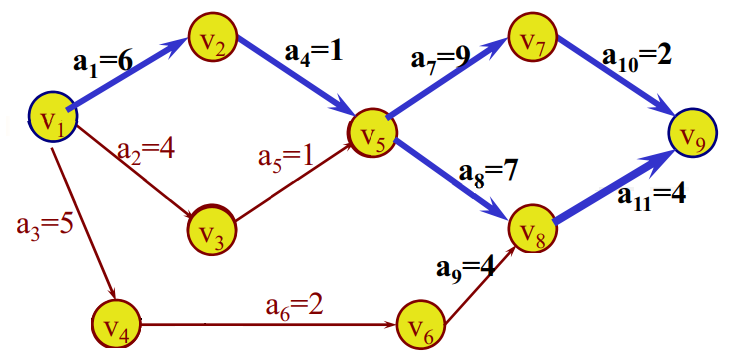
二. 问题分析
-
AOE网的性质:
-
(1)只有在某顶点代表的事件发生后,从该顶点发出去的弧所代表的各项活动才能开始;
-
(2)只有进入某顶点的各条弧所代表的活动都已经结束,该顶点所代表的事件才能发生。
-
求解关键路径需要求解出:事件(顶点)的最早、最迟发生时间;
-
求解关键活动需要求解出:活动(边)的最早、最迟发生时间完成。
-
使用数组
ve、vl分别表示事件的最早、最晚发生时间;使用数组ee、el分别表示活动的最早、最晚发生时间。 -
总体思路:首先求出原图的拓扑序列,然后根据拓扑序推出上述四个数组。
ve数组的求解:事件的最早发生时间
-
ve[start]=0:start为源点,在0时刻就可以开始。 -
事件 $v_i$ 的最早发生时间
ve[i]是从开始顶点 $v_{start}$ 到顶点 $v_i$ 的最长路径长度。 -
按照拓扑序求解:假设在原图中存在一条边
(ver, j),边的权重为w[i],则ve[j] = max(ve[j], ve[ver] + w[i])。
vl数组的求解:事件的最晚发生时间
-
vl[end]=ve[end]:end为汇点。 -
事件 $v_i$ 允许的最晚发生时间
vl[i]是在保证完成顶点 $v_{end}$ 在ve[end]时刻发生的前提下,事件 $v_i$ 允许发生的最晚时间,它等于ve[end]减去 $v_i$ 到 $v_{end}$ 的最长路径长度。 -
按照拓扑序的逆序求解,因此需要使用原图的反向图。假设在反向图中存在一条反向边
(ver, j),边的权重为w[i],则vl[j] = min(vl[j], vl[ver] - w[i])。
根据上述求出的ve、vl数组,我们可以得出关键路径上的点,所有vl[i]-ve[i]==0的点是关键路径上的点,对于上面的例子,我们可以得到下表:
| 顶点 | ve[i] | vl[i] | vl[i]-ve[i] |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 6 | 6 | 0 |
| 3 | 4 | 6 | 2 |
| 4 | 5 | 8 | 3 |
| 5 | 7 | 7 | 0 |
| 6 | 7 | 10 | 3 |
| 7 | 16 | 16 | 0 |
| 8 | 14 | 14 | 0 |
| 9 | 18 | 18 | 0 |
从起点做一遍dfs就可以求出关键路径上的点。
ee数组的求解:活动的最早发生时间
-
在建图的时候,我们每次会在原图和反向图中分别加一条边,边的编号从
0开始,因此0、1,2、3......等都是成对出现的,其中偶数编号的边在原图中,奇数编号的边在反向图中。我们求解原图中的关键边即可。 -
在原图中根据拓扑序求解
ee,如果存在一条(ver, j)的边,边的编号为i,则ee[i]=ve[ver]。
el数组的求解:活动的最晚发生时间
- 需要在反向图中求解
el数组,如果在反向图存在一条(ver, j)的边,边的编号为i,则el[i-1]=vl[ver]-w[i]。这里i-1是因为我们求解的是原图中的关键边。
根据上述求出的ee、el数组,我们可以得出关键路径上的边,所有el[i]-ee[i]==0的边是关键路径上的边,对于上面的例子,我们可以得到下表:
| 活动 | 活动在原图中的编号i | ee[i] | el[i] | el[i]-ee[i] |
|---|---|---|---|---|
| a1 | 0 | 0 | 0 | 0 |
| a2 | 2 | 0 | 2 | 2 |
| a3 | 4 | 0 | 3 | 3 |
| a4 | 6 | 6 | 6 | 0 |
| a5 | 8 | 4 | 6 | 2 |
| a6 | 10 | 5 | 8 | 3 |
| a7 | 12 | 7 | 7 | 0 |
| a8 | 14 | 7 | 7 | 0 |
| a9 | 16 | 7 | 10 | 3 |
| a10 | 18 | 16 | 16 | 0 |
| a11 | 20 | 14 | 14 | 0 |
从起点做一遍dfs就可以求出关键路径上的边。
三. 代码实现
- 这里使用问题描述的图进行测试,测试输入如下:
9 11
1 2 6
1 3 4
1 4 5
2 5 1
3 5 1
4 6 2
5 7 9
5 8 7
6 8 4
7 9 2
8 9 4
-
第一行两个数
n、m,代表图中的点数、边数; -
接下来的
m行,每行有三个数a、b、c表示有一条从a指向b且权重为c的边。 -
默认这里
1号点为源点,n号点为汇点。
只求解关键路径
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
const int N = 1010, M = 100010;
int n, m;
int hs[N], ht[N], e[M], w[M], ne[M], idx; // 顶点表示事件,边表示活动
int ve[N], vl[N]; // 事件允许的最早发生时间, 事件允许的最晚发生时间
// int ee[M], el[M]; // 活动的最早发生时间, 活动的最晚发生时间
int d[N]; // 每个点的入度
int q[N]; // 拓扑排序数组
vector<int> path;
vector<vector<int>> res;
void add(int h[], int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
void topsort() {
int hh = 0, tt = 0;
q[0] = 1;
while (hh <= tt) {
int t = q[hh++];
for (int i = hs[t]; ~i; i = ne[i]) {
int j = e[i];
if (--d[j] == 0)
q[++tt] = j;
}
}
}
void critical_path() {
topsort();
// 求解事件允许的最早发生时间
ve[1] = 0;
for (int k = 0; k < n; k++) {
int ver = q[k];
for (int i = hs[ver]; i != -1; i = ne[i]) {
int j = e[i];
ve[j] = max(ve[j], ve[ver] + w[i]);
}
}
// 求解事件允许的最晚发生时间
memset(vl, 0x3f, sizeof vl);
vl[n] = ve[n];
for (int k = n - 1; k >= 0; k--) {
int ver = q[k];
for (int i = ht[ver]; i != -1; i = ne[i]) {
int j = e[i];
vl[j] = min(vl[j], vl[ver] - w[i]);
}
}
}
void dfs(int u) {
path.push_back(u);
if (hs[u] == -1) {
res.push_back(path);
}
for (int i = hs[u]; ~i; i = ne[i]) {
int j = e[i];
if (vl[j] - ve[j] == 0)
dfs(j);
}
path.pop_back();
}
int main() {
cin >> n >> m;
memset(hs, -1, sizeof hs);
memset(ht, -1, sizeof ht);
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
add(hs, a, b, c);
add(ht, b, a, c);
d[b]++;
}
// 输入满足1号点是源点,n号点是汇点
critical_path();
dfs(1);
for (auto &t : res) {
for (int i = 0; i < t.size(); i++)
cout << t[i] << ' ';
cout << endl;
}
return 0;
}
结果如下(关键路径经过的点):
1 2 5 8 9
1 2 5 7 9
求解关键路径 和 关键活动
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
const int N = 1010, M = 100010;
int n, m; // 顶点数、边数
int hs[N], ht[N], e[M], w[M], ne[M], idx; // 顶点表示事件,边表示活动
int ve[N], vl[N]; // 事件允许的最早发生时间, 事件允许的最晚发生时间
int ee[M], el[M]; // 活动的最早发生时间, 活动的最晚发生时间
int d[N]; // 每个点的入度
int q[N]; // 拓扑排序数组
// 存储关键路径上的点
vector<int> path;
vector<vector<int>> res;
// 存储关键路径上的边
vector<int> edge;
vector<vector<int>> edges;
void add(int h[], int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
void topsort() {
int hh = 0, tt = 0;
q[0] = 1;
while (hh <= tt) {
int t = q[hh++];
for (int i = hs[t]; ~i; i = ne[i]) {
int j = e[i];
if (--d[j] == 0)
q[++tt] = j;
}
}
}
void critical_path() {
topsort();
// 求解事件允许的最早发生时间
ve[1] = 0;
for (int k = 0; k < n; k++) {
int ver = q[k];
for (int i = hs[ver]; i != -1; i = ne[i]) {
int j = e[i];
ve[j] = max(ve[j], ve[ver] + w[i]);
}
}
// 求解事件允许的最晚发生时间
memset(vl, 0x3f, sizeof vl);
vl[n] = ve[n];
for (int k = n - 1; k >= 0; k--) {
int ver = q[k];
for (int i = ht[ver]; i != -1; i = ne[i]) {
int j = e[i];
vl[j] = min(vl[j], vl[ver] - w[i]);
}
}
// 求解活动的最早发生时间
for (int k = 0; k < n; k++) {
int ver = q[k];
for (int i = hs[ver]; i != -1; i = ne[i]) { // (ver, j), 正向边为i
ee[i] = ve[ver];
}
}
// 求解活动的最晚发生时间
for (int k = n - 1; k != -1; k--) {
int ver = q[k];
for (int i = ht[ver]; i != -1; i = ne[i]) { // (ver, j), 反向边为i
el[i - 1] = vl[ver] - w[i]; // i-1是原图中边的编号
}
}
}
void dfs_v(int u) {
path.push_back(u);
if (hs[u] == -1) {
res.push_back(path);
}
for (int i = hs[u]; ~i; i = ne[i]) {
int j = e[i];
if (vl[j] - ve[j] == 0)
dfs_v(j);
}
path.pop_back();
}
void dfs_e(int u) {
if (hs[u] == -1) {
edges.push_back(edge);
}
for (int i = hs[u]; ~i; i = ne[i]) {
int j = e[i];
if (el[i] - ee[i] == 0) {
edge.push_back(w[i]);
dfs_e(j);
edge.pop_back();
}
}
}
void out() {
cout << endl;
// 输出上述分析中的ve、vl数组
cout << "ve : ";
for (int i = 1; i <= n; i++) cout << ve[i] << ' ';
cout << endl;
cout << "vl : ";
for (int i = 1; i <= n; i++) cout << vl[i] << ' ';
cout << endl;
cout << "vl - ve : ";
for (int i = 1; i <= n; i++) cout << vl[i] - ve[i] << ' ';
cout << endl;
cout << "-------------------------------" << endl;
// 输出上述分析中的ee、el数组
cout << "ee : ";
for (int i = 0; i < idx; i += 2) cout << ee[i] << ' ';
cout << endl;
cout << "el : ";
for (int i = 0; i < idx; i += 2) cout << el[i] << ' ';
cout << endl;
cout << "el - ee : ";
for (int i = 0; i < idx; i += 2) cout << el[i] - ee[i] << ' ';
cout << endl;
}
int main() {
cin >> n >> m;
memset(hs, -1, sizeof hs);
memset(ht, -1, sizeof ht);
for (int i = 0; i < m; i++) {
int a, b, c;
cin >> a >> b >> c;
add(hs, a, b, c);
add(ht, b, a, c);
d[b]++;
}
// 输入满足1号点是源点,n号点是汇点
critical_path();
dfs_v(1); // 求解关键路径上的点
dfs_e(1); // 求解关键路径上的边
// 输出关键路径 以及关键路径上的权值
int cnt = res.size(); // 一共cnt条关键路径
for (int i = 0; i < cnt; i++) {
// 先输出边的上权值
auto cri_edge = edges[i];
cout << " ";
for (auto t : cri_edge)
cout << t << " ";
cout << endl;
// 输出顶点
auto cri_node = res[i];
cout << cri_node[0];
for (int i = 1; i < cri_node.size(); i++)
cout << " -> " << cri_node[i];
cout << endl;
}
// 输出上述分析的两个表
out();
return 0;
}
结果如下:
6 1 7 4
1 -> 2 -> 5 -> 8 -> 9
6 1 9 2
1 -> 2 -> 5 -> 7 -> 9
ve : 0 6 4 5 7 7 16 14 18
vl : 0 6 6 8 7 10 16 14 18
vl - ve : 0 0 2 3 0 3 0 0 0
-------------------------------
ee : 0 0 0 6 4 5 7 7 7 16 14
el : 0 2 3 6 6 8 7 7 10 16 14
el - ee : 0 2 3 0 2 3 0 0 3 0 0
结果分析:



orz
很qian~
萌新大受震撼