原题链接
更好的阅读体验

题目描述

达达在买回家的火车票，因为正值春运，售票处排起了长队。

因为晚上室内光线很暗，所以很多人趁机插队。

现在给每个人赋予一个整数作为编号，告诉你每一个排队的人的编号，和他进入队列时的具体位置。

请你确定最终的队列顺序。

输入格式
输入可能包含多组测试用例。

对于每组测试用例，第一行包含整数$N$，表示排队的总人数。

接下来$N$行，每行两个整数$P_i,V_i$，第i行数据表示第i个人进入队列时的位置以及他的个人编号。

一个人的$P_i$值具体表示为当该人员进入队列时，他前面的人数。

例如，如果一个人插到了队首，则其$P_i$值为0，如果插到了第三个位置（第二个人后面），则其$P_i$值为2。

输出格式
每个测试用例，输出一行包含N个整数（表示每个人的编号）的结果，表示最终的人员队列顺序。

每个结果占一行，同行数据之间空格隔开。

数据范围
$1 \le N \le 200000$,
$0 \le V_i \le 32767$,
$0 \le P_i \le i-1$

样例

输入样例：
4
0 77
1 51
1 33
2 69
4
0 20523
1 19243
1 3890
0 31492
输出样例：
77 33 69 51
31492 20523 3890 19243

样例解释
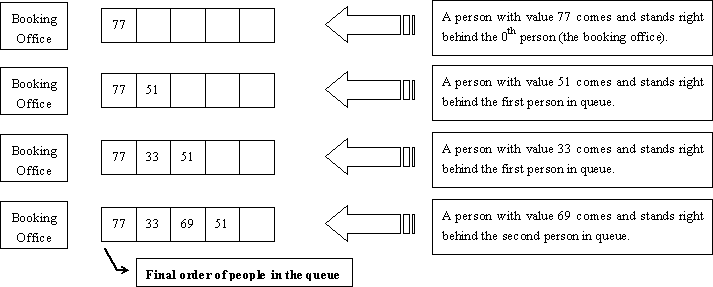
下图描述了输入样例中第一组测试用例的场景。

树状数组

如果你足够机智的话,你就会发现这道题目,非常优秀地和之前谜一样的牛的思路是一模一样,没有任何区别.

题面
谜一样的牛题解

我们发现,如果说当前第$K$个人的前面有$A_k$个人,那么它的位置$H_k$就是数值$1~n$中第$A_k+1$小的没有在${H_{k+1},H_{k+2},…,H_n}$中出现过的数.(瞧瞧我这复制黏贴)

所以说,我们需要建立一个长度为n的1序列b,刚开始都是1,然后n到1倒序扫描每一个$A_i$,对于每个$A_i$执行查询和修改操作.

也就是说这道题目的题意就是让我们,动态维护一个01序列,支持查询第k个1所在的位置,以及修改序列中的一个数值

这道题目证明了一点,事实总是惊人的相似,历史总是会不断地重演.原题从来都不缺改题目背景描述.

C++ 代码

#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
const int N=200000+100;
int a[N],c[N],n,m,i,j,k,ans[N],p[N],v[N];
inline int ask(int x)
{
    int ans=0;
    for(;x;x-=lowbit(x))
        ans+=c[x];
    return ans;
}
inline int add(int x,int y)
{
    for(;x<=n;x+=lowbit(x))
        c[x]+=y;
}
int main()
{
    ios::sync_with_stdio(false);
    while(cin>>n)
    {
        memset(c,0,sizeof(c));
        for(int i=1;i<=n;i++)
        {
            cin>>p[i]>>v[i];
            p[i]++;
            add(i,1);
        }
        for(int i=n;i>=1;i--)
        {
            int l=1,r=n;
            while(l<r)
            {
                int mid=(l+r)>>1;
                if (ask(mid)<p[i])
                    l=mid+1;
                else
                    r=mid;
            }
            ans[r]=v[i];
            add(r,-1);
        }
        for(i=1;i<=n;i++)
            cout<<ans[i]<<" ";
        cout<<endl;
    }
    return 0;
}