思路

暴力的方法是$O(NM)$时间复杂度。画个图出来就能知道哪里有优化的空间。

以 1 2 4 7 和 3 4 6 8 为例，画二维矩阵，(i,j) 位置上是 a[i] + b[j] 与目标和 x 的关系， $L$ 代表小于，$G$ 代表大于，对勾是正好相等。

在暴力扫描这个二维矩阵的时候，一旦发现某个位置 (i,j) 是 $G$ ，那就可以肯定在 (i,j) 右下方的所有矩阵元素都是 $G$，因此也可以知道在目标和元素左上方的所有元素都是 $L$。

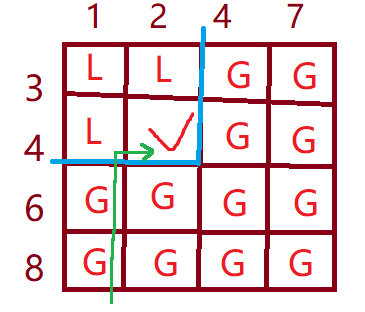
所以其实不用扫描整个矩阵，只要从一个合适的角落出发，到达了蓝色的边界线沿着这条线找，就可以很容易地摸到目标和元素的位置。这个复杂度是$O(N+M)$。

代码

#include <iostream>
using namespace std;

const int N = 1e5 + 10;

int n, m;
int a[N], b[N];

int main() {

  int x;
  cin >> n >> m >> x;

  for (int i = 0; i < n; i ++ ) cin >> a[i];
  for (int i = 0; i < m; i ++ ) cin >> b[i];

  for (int i = 0, j = m - 1; i < n; i ++ ) {
    while (j >= 0 && a[i] + b[j] > x) j -- ;
    if (a[i] + b[j] == x) {
      cout << i << ' ' << j;
      break;
    }
  }
}