算法分析

本来是一个dfs的过程，遍历所有的位置，找到从当前位置往下走的最大路径，再取最大值，可是这样做会有很多重复的位置被重新计算过，因此可以利用空间换时间的思想，把遍历过的位置往下走的路径的最大值进行记录，这就是记忆化搜索

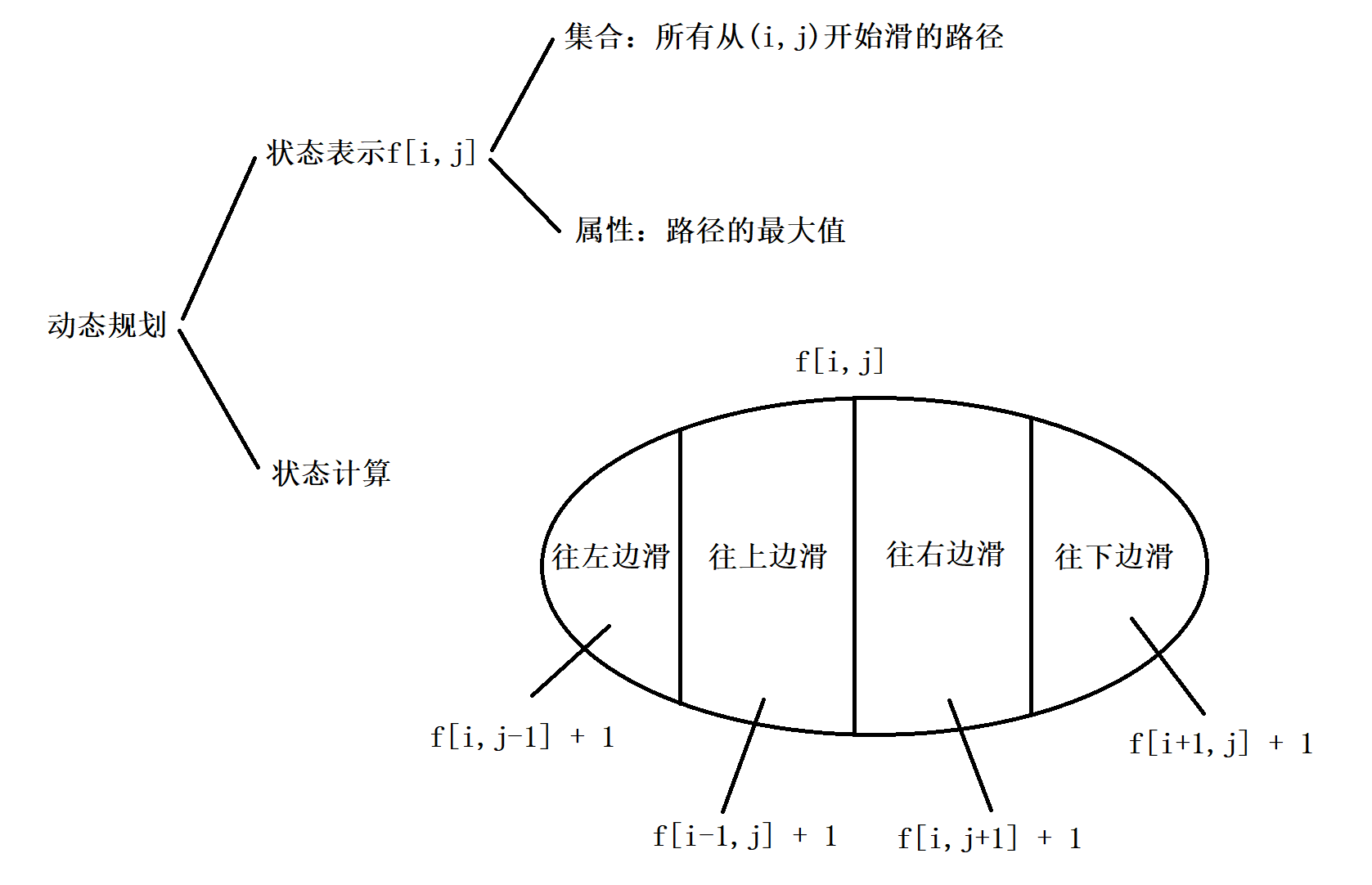
注意：f[][]二维数组初始化的时候最好统一赋值为-1，如果不进行初始化直接用0判断，此题可以，可是如果遇到一些记忆化搜索的问题要求方案数的时候，初始化是0可能会导致个别情况计算出来的恰好结果是0时，却被认为未遍历过，因此统一赋值为-1就没错了

时间复杂度 $O(n^2)$

参考文献

算法基础课

Java 代码

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int N = 310;
    static int n,m;
    static int[][] h = new int[N][N];
    static int[][] f = new int[N][N];
    static int[] dx = new int[] {0,-1,0,1};
    static int[] dy = new int[] {-1,0,1,0};
    static int dfs(int x,int y)
    {
        if(f[x][y] != -1) return f[x][y];

        f[x][y] = 1;
        for(int i = 0;i < 4;i ++)
        {
            int a = x + dx[i];
            int b = y + dy[i];
            if(a < 0 || a >= n || b < 0 || b >= m) continue;
            if(h[x][y] > h[a][b]) f[x][y] = Math.max(f[x][y], dfs(a,b) + 1);
        }
        return f[x][y];
    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        m = scan.nextInt();
        for(int i = 0;i < n;i ++)
        {
            for(int j = 0;j < m;j ++)
                h[i][j] = scan.nextInt();
        }

        for(int i = 0;i < n;i ++) Arrays.fill(f[i], -1);

        int res = 0;
        for(int i = 0;i < n;i ++)
        {
            for(int j = 0;j < m;j ++)
            {
                res = Math.max(res, dfs(i,j));
            }
        }
        System.out.println(res);
    }
}

题目：等和的分隔子集

在某客的一道关于记忆化搜索求方案数的问题

题目描述

算法分析

本身这题是一个dfs的题目，从1到n中枚举，有两种方法，要么放左边left，要么放右边right，最终枚举完时若left == right，则表示当前情况成立，ans ++，可是N = 39,2^39远大于10^8，因此直接dfs会直接gg掉，又由于枚举到当前状态x,left,right时，当前状态成立的方案数一定是固定的，因此可以用一个数组存储当前状态的值，空间换时间，于是采用记忆化搜索的方法

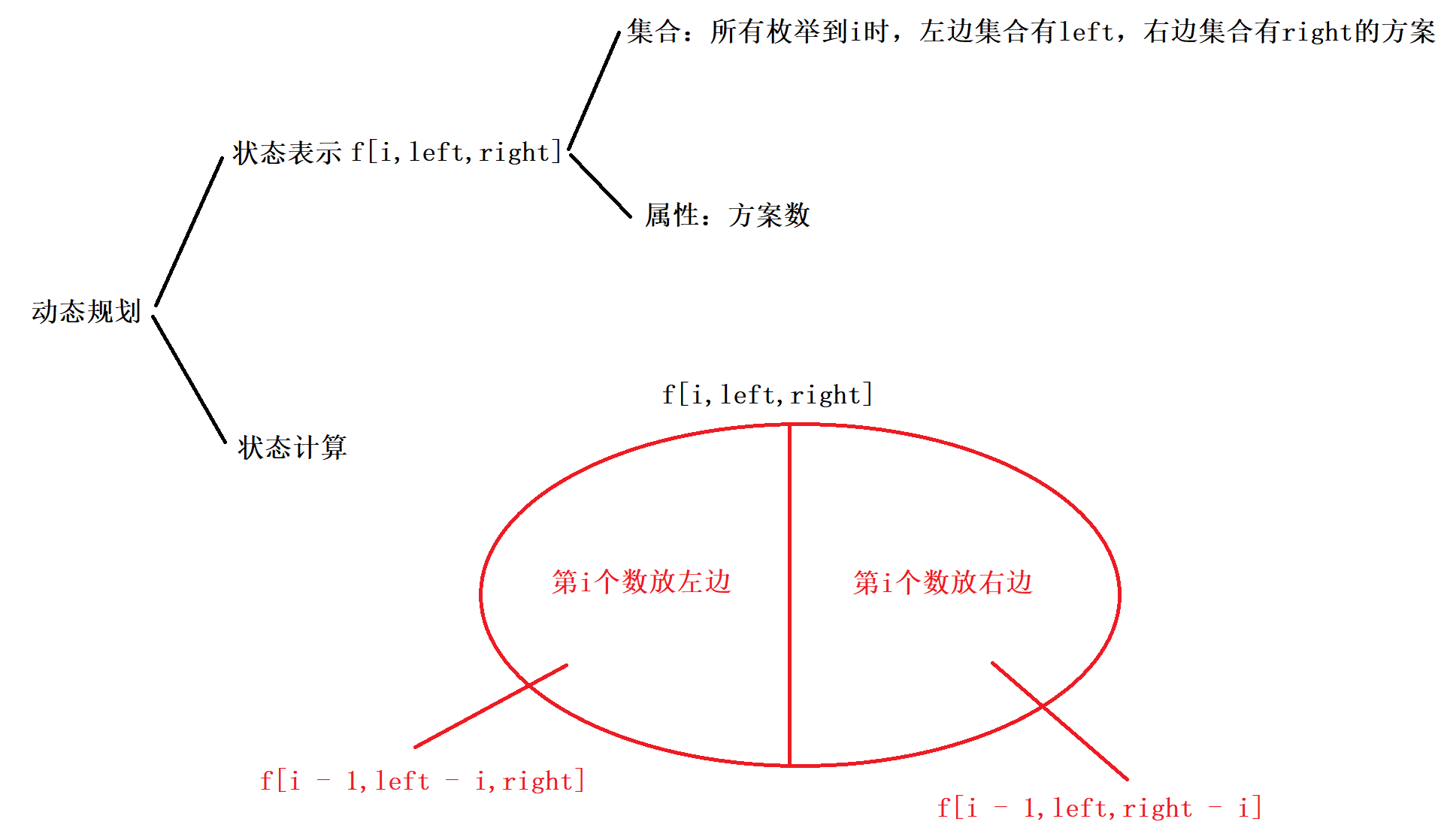
初始时，f[0][0][0] = 1;其他全是-1，为了方便排除方案数刚刚是0的情况(例如当n == 37时，就是方案数为0的情况)，由于N = 39，最大的累加和是(1 + 39) * 40 / 2 == 800，分成左右两个集合，因此每个集合最多是400，因此开f[40][400][400]的空间

注意：由于左右集和总和相等时可以看成等价，因此求出来的结果会产生重复，因此需要除以2

时间复杂度

远小于40 * 400 * 400

Java 代码

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int N = 410;
    static int n;
    static int ans = 0;
    static long[][][] f = new long[40][N][N];
    static long dfs(int x,int left,int right)
    {

        if(f[x][left][right] != -1) return f[x][left][right];

        f[x][left][right] = 0;
        if(x <= 0) return f[x][left][right];

        if(left - x >= 0) f[x][left][right] += dfs(x - 1,left - x,right);
        if(right - x >= 0) f[x][left][right] += dfs(x - 1,left,right - x);

        return f[x][left][right];
    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        int m = (1 + n) * n / 2; 

        for(int i = 0;i <= n;i ++)
            for(int j = 0;j <= m / 2;j ++)
                Arrays.fill(f[i][j], -1);

        f[0][0][0] = 1;

        System.out.println(dfs(n,m / 2,m / 2) / 2);
    }
}

会超时的爆搜

时间复杂度$O(2^n)$

Java 代码

import java.util.Scanner;

public class Main {
    static int ans = 0;
    static int n;
    static void dfs(int x,int left,int right)
    {
        if(x == n + 1)
        {
            if(left == right) ans ++;
            return ;
        }
        //放左边
        dfs(x + 1,left + x,right);

        //放右边
        dfs(x + 1,left,right + x);
    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        dfs(1,0,0);
        System.out.println(ans / 2);
    }
}