题目描述

给定一个 $n$ 个点 $n - 1$ 条边的无向无权连通图(无根树)

求加一条边或两条边的 $dfs$ 序遍历图的最小路径长度，新加的边要走且只能走一次

参考了@秦淮岸灯火阑珊 dalao的题解

如果不加边，那么每条路径来回要走两边，答案就是 $2(n - 1)$

如果在两个点之间加了一条边，那么就可以省去在原本的树中，两个点之间的路径

设路径长度为 $d$，答案就是 $2(n - 1) - d + 1$

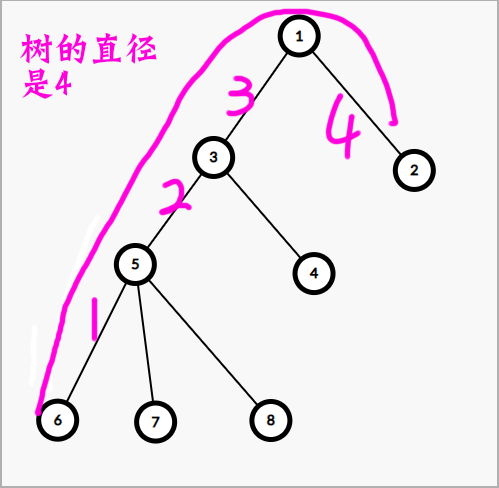
如图所示 图也是偷qha大佬的

本来 $2$ 号点到 $6$ 号点的路径上的每条边需要走两次，加了这条边之后，遍历完其中一个子树可以通过这条边直达另一个点，这条路径上的所有边就可以少走一次。

显然，如果只加一条边的话，两个点之间的路径越长越好，我们取最长的路径，也就是 树的直径，即为加一条边的最优解。

上周写了一半的题解，然后就忘了
加两条边时为什么要把直径上的边权都设成-1好像还没想通qaq
先发出来算了反正能AC就行

时间复杂度 $O(n)$

C++ 代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>

using namespace std;

const int N = 100010, M = N * 2, INF = 0x3f3f3f3f;

int h[N], e[M], w[M], ne[M], idx;
void add(int a, int b)
{
    e[idx] = b;
    w[idx] = 1;
    ne[idx] = h[a];
    h[a] = idx ++;
}

int n, k;
int d[N], path[N];
int q[N];

int bfs(int root)
{
    memset(d, 0x3f, sizeof d);
    d[root] = 0;
    path[root] = -1;

    int hh = 0, tt = -1;
    q[++ tt] = root;

    int res = root;
    while(hh <= tt)
    {
        int u = q[hh ++];

        for(int i = h[u]; ~i; i = ne[i])
        {
            int j = e[i], dist = d[u] + w[i];
            if(d[j] == INF)
            {
                d[j] = dist;
                if(d[j] > d[res])  res = j;
                path[j] = i;

                q[++ tt] = j;
            }
        }
    }
    return res;
}

int d1[N], d2[N], diam;
void dfs(int u, int fa)
{
    d1[u] = d2[u] = 0;
    for(int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if(j == fa)  continue;
        dfs(j, u);

        diam = max(diam, d1[u] + d1[j] + w[i]);

        if(d1[j] + w[i] > d1[u])  d2[u] = d1[u], d1[u] = d1[j] + w[i];
        else if(d1[j] + w[i] > d2[u])  d2[u] = d1[j] + w[i];
    }
}

int main()
{
    memset(h, -1, sizeof h);

    scanf("%d%d", &n, &k);
    for(int i = 1; i < n; i ++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
        add(b, a);
    }

    int a = bfs(1),  b = bfs(a);
    int res = 2 * (n - 1) - d[b] + 1;
    if(k == 2)
    {
        int u = b;
        while(u != a)
        {
            w[path[u]] = w[path[u] ^ 1] = -1;
            u = e[path[u] ^ 1];
        }
        dfs(1, -1);
        res = res - diam + 1;
    }
    printf("%d", res);
    return 0;
}