（1）闫氏DP分析法
$$ DP \begin{cases} 状态表示f[i] \begin{cases} 集合：从前i家偷的所有合法方案 \\\\ 属性：最大收益 \\\\ \end{cases} \\\\ \\\\ 状态计算 \begin{cases} 偷第i家店铺 \to f[i - 2] + w[i] \\\\ 不偷第i家店铺 \to f[i - 1] \\\\ \end{cases} \\\\ \end{cases} \\\\ $$

#include <iostream>
using namespace std;

const int N = 1e5 + 10;

int n, T;
int w[N], f[N];

int main() {
    cin >> T;
    while (T -- ) {
        cin >> n;
        for (int i = 1; i <= n; i ++ ) cin >> w[i];
        f[1] = w[1];
        for (int i = 2; i <= n; i ++ ) f[i] = max(f[i - 1], f[i - 2] + w[i]);
        cout << f[n] << endl;
    }
    return 0;
}

（2）状态机

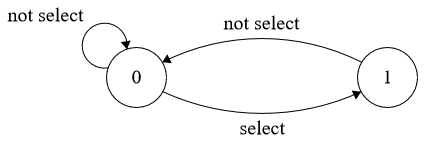
• 0: 未选最后一个店铺
• 1: 选最后一个店铺

$$ DP \begin{cases} 状态表示f[i, 0], f[i, 1] \begin{cases} 集合：所有走了i步，且当前位于状态j（0/1）的所有走法 \\\\ 属性：最大收益 \\\\ \end{cases} \\\\ \\\\ 状态计算 \begin{cases} f[i, 0] \begin{cases} 最后一步从0到0 \to f[i - 1, 0] \\\\ 最后一步从1到0 \to f[i - 1, 1] \\\\ \end{cases} \\\\ f[i, 1]：只有一种走法，最后一步从0到1 \to f[i - 1, 0] + w[i] \\\\ \end{cases} \\\\ \end{cases} \\\\ $$

#include <iostream>
using namespace std;

const int N = 1e5 + 10, INF = 0x3f3f3f3f;

int n, T;
int w[N], f[N][2];

int main() {
    cin >> T;
    while (T -- ) {
        cin >> n;
        for (int i = 1; i <= n; i ++ ) cin >> w[i];
        f[0][0] = 0, f[0][1] = -INF; // 入口只能从0开始
        for (int i = 1; i <= n; i ++ ) {
            f[i][0] = max(f[i - 1][0], f[i - 1][1]);
            f[i][1] = f[i - 1][0] + w[i];
        }
        cout << max(f[n][0], f[n][1]) << endl; // 答案是偷最后一家或者不偷最后一家店，二者种的较大者
    }
    return 0;
}