$$ \texttt{Preface} $$
$$ \texttt{Description} $$
有一个名为 233 的矩阵 $a$。
对于第一行,有 $a_{0, 1} = 233$,$a_{0, 2} = 2333$,$a_{0,3} = 23333$ …
对于 $\forall i, j \neq 0$,有 $a_{i,j} = a_{i-1, j} + a_{i, j - 1}$。
给出 $a_{1, 0}, a_{2, 0}, …, a_{n, 0}$,请在 233 矩阵中求出 $a_{n, m}$。
$$
\texttt{Solution}
$$
不妨设 $a_{0,0} = 23$。
对 $a_{i, j} = a_{i - 1, j} + a_{i, j - 1}$ 这个式子比较熟悉的巨佬们应该都知道:
$$
a_{i, j} = \sum\limits_{k = 1}^{i} a_{k, j - 1} + a_{0, j}
$$
特别地:
$$
a_{0, j} = 10 \times a_{0, j - 1} + 3
$$
则有:
$$
a_{i, j} = \sum\limits_{k = 1}^{i} a_{k, j - 1} + 10 \times a_{0, j - 1} + 3
$$
观察上式,注意到第 $j$ 列每个位置上的值都可以由第 $j - 1$ 列的若干个项递推而来,又注意到 $n \leq 10$,$m \leq 10^9$,于是考虑矩阵乘法加速递推。
设 $F(j) = \begin{bmatrix} a_{0, j} & a_{1, j} & \cdots & a_{n, j} & 3 \end{bmatrix}$,则有:
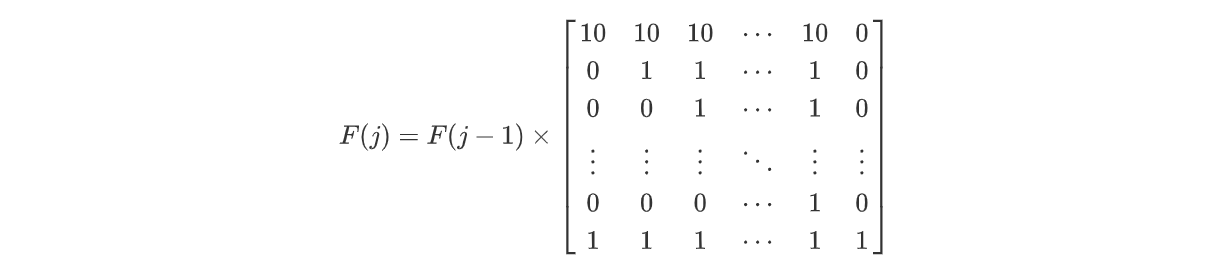
(因为 AcWing 矩阵显示可能有点问题,只好放图片了)
设转移矩阵为 $G$,则 $F(m) = F(0) \times G^m$。
时间复杂度 $\mathcal{O(n^3 \log m)}$。
$$
\texttt{Code}
$$
#include <cstdio>
#include <cstring>
using namespace std;
namespace IO {
static char buf[1 << 20], *fs, *ft;
inline char gc() {
if (fs == ft) {
ft = (fs = buf) + fread(buf, 1, 1 << 20, stdin);
if (fs == ft) return EOF;
}
return *fs ++;
}
#define gc() getchar()
inline int read() {
int x = 0, f = 1; char s = gc();
while (s < '0' || s > '9') {if (s == '-') f = -f; s = gc();}
while (s >= '0' && s <= '9') {x = x * 10 + s - '0'; s = gc();}
return x * f;
}
} using IO :: read;
const int N = 110;
const int mod = 1e7 + 7;
int n, m;
int f[N];
int G[N][N];
void mul(int d[N][N], int a[N][N], int b[N][N]) {
static int c[N][N]; memset(c, 0, sizeof(c));
for (int i = 0; i <= n + 1; i ++)
for (int j = 0; j <= n + 1; j ++)
for (int k = 0; k <= n + 1; k ++)
c[i][j] = (c[i][j] + 1ll * a[i][k] * b[k][j]) % mod;
memcpy(d, c, sizeof(c));
}
void mulstar(int d[N], int a[N], int b[N][N]) {
static int c[N]; memset(c, 0, sizeof(c));
for (int j = 0; j <= n + 1; j ++)
for (int k = 0; k <= n + 1; k ++)
c[j] = (c[j] + 1ll * a[k] * b[k][j]) % mod;
memcpy(d, c, sizeof(c));
}
void work() {
f[0] = 23;
for (int i = 1; i <= n; i ++) f[i] = read();
f[n + 1] = 3;
for (int j = 0; j <= n; j ++) {
G[0][j] = 10;
for (int i = 1; i <= n; i ++)
if (i <= j) G[i][j] = 1;
else G[i][j] = 0;
}
for (int i = 0; i <= n; i ++)
G[i][n + 1] = 0;
for (int j = 0; j <= n + 1; j ++)
G[n + 1][j] = 1;
for (int b = m; b; b >>= 1) {
if (b & 1) mulstar(f, f, G);
mul(G, G, G);
}
printf("%d\n", f[n]);
}
int main() {
while (scanf("%d%d", &n, &m) != EOF) work();
return 0;
}
$$ \texttt{Thanks} \ \texttt{for} \ \texttt{reading} $$


%%%
excellent job!