题目描述

农夫约翰希望为他的奶牛们建立一个畜栏。

这些挑剔的畜生要求畜栏必须是正方形的，而且至少要包含C单位的三叶草，来当做它们的下午茶。

畜栏的边缘必须与X，Y轴平行。

约翰的土地里一共包含N单位的三叶草，每单位三叶草位于一个1 x 1的土地区域内，区域位置由其左下角坐标表示，并且区域左下角的X,Y坐标都为整数，范围在1到10000以内。

多个单位的三叶草可能会位于同一个1 x 1的区域内，因为这个原因，在接下来的输入中，同一个区域坐标可能出现多次。

只有一个区域完全位于修好的畜栏之中，才认为这个区域内的三叶草在畜栏之中。

请你帮约翰计算一下，能包含至少C单位面积三叶草的情况下，畜栏的最小边长是多少。

输入格式
第一行输入两个整数 C 和 N。

接下来 N 行，每行输入两个整数 X 和 Y，代表三叶草所在的区域的X,Y坐标。

同一行数据用空格隔开。

输出格式
输出一个整数，代表畜栏的最小边长。

数据范围
1≤C≤500,
C≤N≤500

样例

输入样例：
3 4
1 2
2 1
4 1
5 2
输出样例：
4

二分

基本思想：每一个x,y的数据范围为1~10000，对于1~10000做二分，对每个长度检查是否可以满足条件。

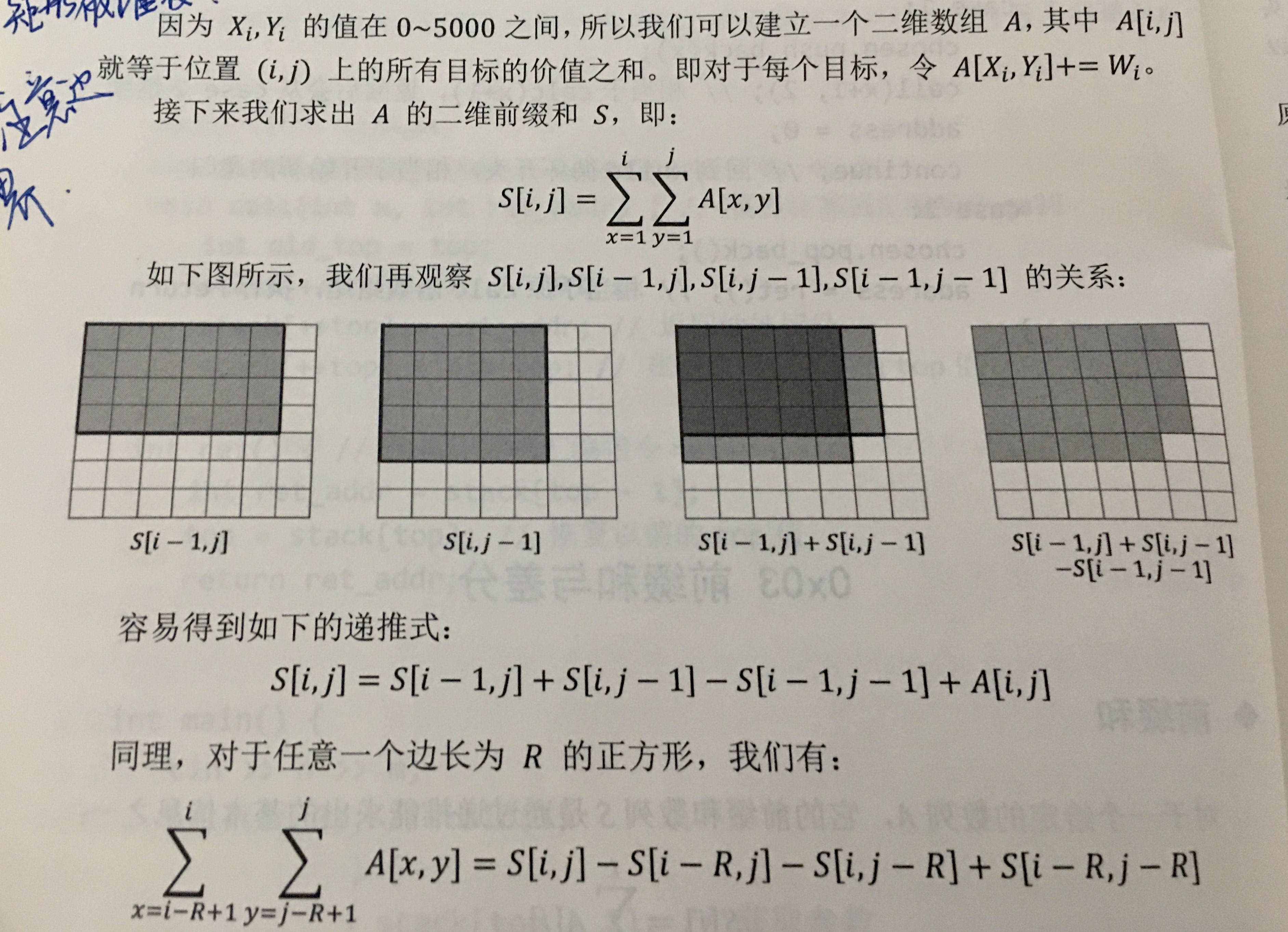
在枚举正方形的时候，想要满足条件，那么正方形至少有一条边上是有三叶草的点的，否则这个正方形就可以缩小，直到有点为止，所以可以枚举所有的矩形，利用前缀和可以以O(1)的时间得到任意大小的方形内有多少三叶草。

如果用数据的范围10000来枚举，那么10^8，会超时，而所有的有三叶草的点最多500个，那么不同的x,y的值最多有1000个，那么将这1000个数映射到一个连续的集合，再进行枚举就是10^6。

所以思路变为在进行离散化处理后，计算前缀和，再二分，看以mid为边长的矩形是否符合条件。
但是在离散化之后，两个相邻的值之间的距离可能不是1，所以在计算距离的时候要先通过这个离散化后的值找到原来是多少，再进行计算

C++ 代码

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

typedef pair<int,int>PII;
const int N=1010;

int n,c;
int sum[N][N];
PII points[N];
vector<int>num;

int dis(int x){
    int l=0,r=num.size()-1;
    while(l<r){
        int mid=(l+r)>>1;
        if(num[mid]>=x)  r=mid;
        else l=mid+1;
    }
    return r;
}
int check(int len){
    //这个区间长度只要小于等于len，并且其中的三叶草数目可以>=c即可
    //x2-x1和y2-y1的长度可以不相等，因为他们都<=len并且三叶草数目>=c，就算长度不相等，在边长为len的正方形中也是可以满足条件的
    for(int x1=1,x2=1;x2<num.size();x2++){//注意开始时x1,x2都是1
        //初始时正方形边长
        while(num[x2]+1-num[x1]>len) x1++;//num[x2]+1是因为(x,y)表示的是三叶草的左下角，所以要把这整个方格包含进来再计算
        for(int y1=1,y2=1;y2<num.size();y2++){
            while(num[y2]+1-num[y1]>len) y1++;
            if(sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1]>=c)//要注意-1
                return 1;
        }
    }
    return 0;
}
int main(){
    cin>>c>>n;
    num.push_back(0);//从0开始
    for(int i=0;i<n;i++){
        int x,y;
        cin>>x>>y;
        points[i]={x,y};
        num.push_back(x);
        num.push_back(y);
    }

    sort(num.begin(),num.end());
    //erase，输入两个迭代器，删除[起始迭代器，结束迭代器)之间的元素
    //unique，输入两个迭代器，将重复的元素放到最后，返回第一个重复的数的位置
    num.erase(unique(num.begin(),num.end()),num.end());
    //离散化,二分找到当前值在离散化后的坐标
    for(int i=0;i<n;i++){
        int x=dis(points[i].first);
        int y=dis(points[i].second);
        sum[x][y]++;//此时存的还是此点存在的三叶草数目
    }
    //求出前缀和
    for(int i=1;i<num.size();i++){
        for(int j=1;j<num.size();j++){
            sum[i][j]+=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
        }
    }
    //二分答案
    int l=1,r=10000;
    while(l<r){
        int mid=(l+r)>>1;
        if(check(mid)) r=mid;
        else l=mid+1;
    }
    cout<<r<<endl;
    return 0;
}