Alice和Bob玩了一个古老的游戏:首先画一个 n×n 的点阵(下图 n=3 )。
接着,他们两个轮流在相邻的点之间画上红边和蓝边:
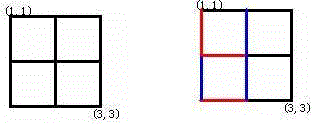
直到围成一个封闭的圈(面积不必为 1)为止,“封圈”的那个人就是赢家。因为棋盘实在是太大了,他们的游戏实在是太长了!
他们甚至在游戏中都不知道谁赢得了游戏。
于是请你写一个程序,帮助他们计算他们是否结束了游戏?
输入格式
输入数据第一行为两个整数 n 和 m。n表示点阵的大小,m 表示一共画了 m 条线。
以后 m 行,每行首先有两个数字 (x,y),代表了画线的起点坐标,接着用空格隔开一个字符,假如字符是 D,则是向下连一条边,如果是 R 就是向右连一条边。
输入数据不会有重复的边且保证正确。
输出格式
输出一行:在第几步的时候结束。
假如 m 步之后也没有结束,则输出一行“draw”。
数据范围
1≤n≤200,
1≤m≤24000
输入样例:
3 5
1 1 D
1 1 R
1 2 D
2 1 R
2 2 D
输出样例:
4
算法思路:
该题实际上可以看作是一个图型结构,然后需要我们计算可以形成一个连通分量所需要的最少步数,题目中的每一步就相当于一条线段,我们就是要对线段的两个端点进行处理就好了。该端点又与常规的并查集操作中的点有所不同,其是按坐标表示,常规的是一个数表示,观察题目可以发现,这些点都是在一个矩阵中,那么这个矩阵中的点可以按照从左到右从上到下的方法排序,该顺序可以可以和左边建立起关系:(x-1)*矩阵大小+y,这样就可以将坐标转化为一个数做该点的索引。剩下的就是进行并查集操作,检查每次走的步的两个端点是否有相同的祖先结点,如果没有就将两个变为一个集合,如果有那么就找到了一个连通分量,将当前所走过的步直接输出就可以得到结果。
算法描述:
- 判断每次输入的步(x,y,direction)的方向direction,如果向下(即D),那么该步的两个端点为(x,y)和(x+1,y),如果向右(即R),那么两个端点为(x,y)和(x,y+1);
- 查找两个端点的祖先结点,如果不相等,那么将其中一个端点的祖先结点改为另一个端点的祖先结点,如果相等,输出当前所走步数。
源代码(已AC):
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
int father[40010];
int findFather(int x)
{
if(x==father[x]) //查找祖先结点
return x;
else //路径压缩
{
int F=findFather(father[x]); //F为祖先结点
father[x]=F;
return F;
}
}
int main()
{
int S,N;
int x,y;
char T;
int x1,y1,idx1,idx2,faA,faB;
cin>>S>>N;
for(int i=1;i<=S*S;i++)
father[i]=i; //每个结点初始化为自身的祖先结点
for(int i=1;i<=N;i++)
{
cin>>x>>y>>T;
if(T=='D')
{
x1=x+1;
y1=y;
idx1=(x-1)*S+y; //根据坐标计算其再father[]中的位置
idx2=(x1-1)*S+y1;
faA=findFather(idx1);
faB=findFather(idx2);
if(faA!=faB) //判断祖先节点是否相同
father[idx2]=faA;
else
{
cout<<i;
return 0;
}
}
if(T=='R')
{
x1=x;
y1=y+1;
idx1=(x-1)*S+y;
idx2=(x1-1)*S+y1;
faA=findFather(idx1);
faB=findFather(idx2);
if(faA!=faB)
father[idx2]=faA;
else
{
cout<<i;
return 0;
}
}
}
cout<<"draw"; //如果走完所有步都没有发现圈,则输出“draw”
return 0;
}


清楚明了,强啊
坐标从1开始怎么对应呢