题目来源：第十届蓝桥杯省赛C++B组

算法标签：二叉树

题目描述：

给定 N 个加号、M 个减号以及 N+M+1 个整数 A1,A2,⋅⋅⋅,AN+M+1，小明想知道在所有由这 N 个加号、M 个减号以及 N+M+1 个整数凑出的合法的后缀表达式中，结果最大的是哪一个？

请你输出这个最大的结果。

例如使用 123+−，则 “23+1−” 这个后缀表达式结果是 4，是最大的。

输入格式

第一行包含两个整数 N 和 M。

第二行包含 N+M+1 个整数 A1,A2,⋅⋅⋅,AN+M+1。

输出格式

输出一个整数，代表答案。

数据范围

0≤N,M≤10E5,
−109≤Ai≤10E9

思路

我们有N个加号，M个减号，拼凑最大的一个后缀表达式。
则我们从后缀表达式特征入手。

以二叉树后续遍历顺序描绘，则很明显有下面的特征。

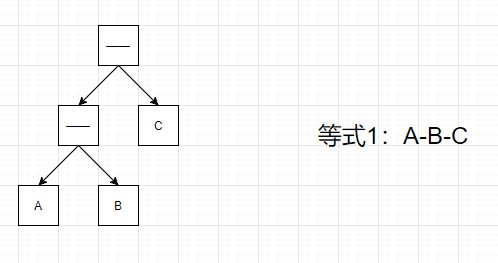
当我们将新的数放到左子树上且新的符号为负数时，会将原有的数据全部取反。

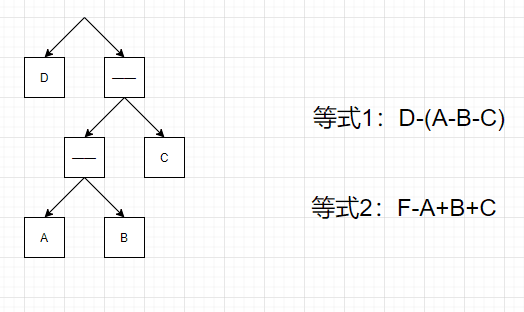
依据这个特征，我们的数据实际上可以自由更改加减，又因为题目要求求最大值，则我们只需要根据以上反转的特性，构造负数，利用一个负数将多个负数都尽可能转换为正值，最终我们只需要加上最大值减去最小值，再添加完所有的中间值即可求到最大的可能。

其中，当m为0，也就是没有负数时，我们不需要实施反转操作，所有的操作都为+，此时我们只需增加所有的数字的绝对值即可。

题目代码

#include<iostream>
#include<algorithm>

using namespace std;

const int N=2E5+10;//因为数据总量实际是M+N+1
int a[N];

int main()
{
    int m,n;
    cin>>n>>m;
    int k = m+n+1;

    for(int i=0;i<k;i++)cin>>a[i];//读入数据
    sort(a,a+k);

    long long res=0;
    if(!m)for(int i=0;i<k;i++)res+=a[i];//如果没有-号
    else 
    {
        res=a[k-1]-a[0];
        for(int i=1;i<k-1;i++)res+=abs(a[i]);
    }

    cout<<res;
    return 0;
}