题目描述

给定 N 个加号、M 个减号以及 N+M+1 个整数 A1,A2,⋅⋅⋅,AN+M+1，小明想知道在所有由这 N 个加号、M 个减号以及 N+M+1 个整数凑出的合法的后缀表达式中，结果最大的是哪一个？

请你输出这个最大的结果。

例如使用 123+−，则 “23+1−” 这个后缀表达式结果是 4，是最大的。

输入格式
第一行包含两个整数 N 和 M。

第二行包含 N+M+1 个整数 A1,A2,⋅⋅⋅,AN+M+1。

输出格式
输出一个整数，代表答案。

数据范围
0≤N,M≤105,
−109≤Ai≤109

样例

输入样例：
1 1
1 2 3
输出样例：
4

在计算机中后缀表达式是最好计算的，将后缀表达式转化为二叉树，再将这颗二叉树后序或前序遍历计算出的结果是相同的，就不存在二义性；二叉树的叶子节点是操作数，非叶子节点都是操作符
这颗二叉树的结果就是左子树的结果与右子树的结果对根节点的操作符运算。

后缀表达式转二叉树
1. 创建一个栈s
2. 如果是操作数就直接入栈
3. 如果是操作符就将栈内的数或符出栈，第一个出栈的是右子节点，第二个是左子节点，再将操作符出栈
4. 最后栈内就在只剩下根节点的操作符

然而这个题根本不用后缀表达式
这个题目不可以从小到大排序后前面减后面加，因为还可以加括号，3-1-2和3-(1-2)是不一样的，所以这个题目最大的坑就在与减号在加括号后可以变成加号，所以着重考虑减号的个数变化。
题目若给出了N个减号，那么在加括号再开括号后，最终留下的减号数可以在1~N中任意变化都可以

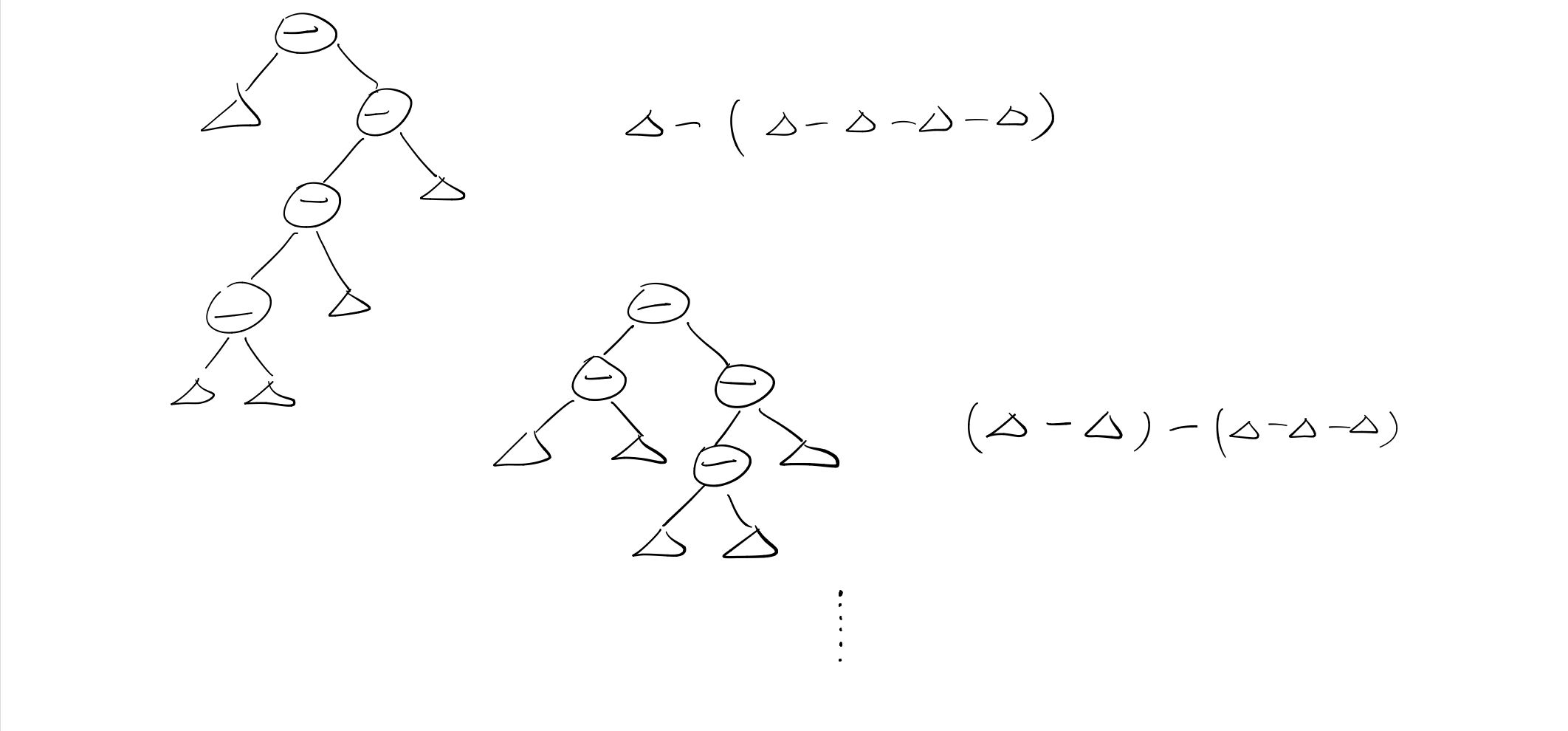
所以分情况考虑：
在减号个数N>0时

1. 负数个数为0，那么最大是留下一个减号，并且减掉最小的那个，那么就是所有数的总和-2*min
2. 负数个数>N，那么，保留所有减号
3. 负数个数为k，在1~N之间，那么留下k个减号即可

C++ 代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 200010;

int n, m;
int a[N];

int main()
{
    scanf("%d%d", &m, &n);
    int k = n + m + 1;
    for (int i = 0; i < k; i ++ ) scanf("%d", &a[i]);

    LL sum = 0;
    if (!n)
    {
        for (int i = 0; i < k; i ++ ) sum += a[i];
    }
    else
    {
        int maxp = 0, minp = 0;
        for (int i = 0; i < k; i ++ )
        {
            if (a[i] > a[maxp]) maxp = i;
            if (a[i] < a[minp]) minp = i;
        }

        sum = a[maxp] - a[minp];
        for (int i = 0; i < k; i ++ )
            if (i != maxp && i != minp)
                sum += abs(a[i]);
    }

    printf("%lld\n", sum);

    return 0;
}