题目描述

给定一个无序的整数数组，找到其中最长上升子序列的长度。

样例

一、算法1：DP

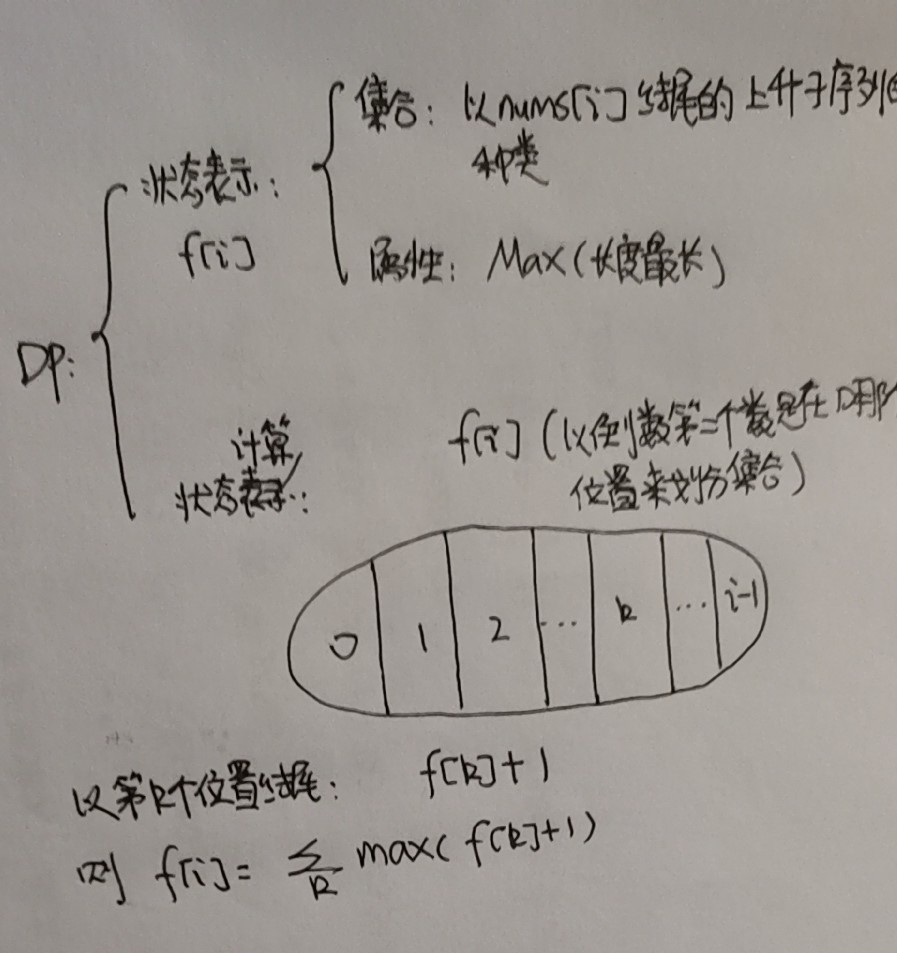
其中计算f[k]时候，f[k]不一定存在，因为是上升子序列，只有当nums[k] < nums[i]时候才能计算！！！

1.1、时间复杂度： 状态数量 x 状态计算 = n * n = O(n^2)

1.2、C++ 代码

class Solution {
public:
    //考点： DP, 时间为O(n^2)
    vector<int> f;
    int lengthOfLIS(vector<int>& nums) {
        if(nums.empty()) return 0;
        int n = nums.size();
        f = vector<int>(n+10);
        for(int i=0; i<n; i++)
        {
            f[i] = 1; //以nums[i]结尾的子序列长度至少是1。
            for(int j=0; j<=i; j++)
            {
                if(nums[i] > nums[j]) f[i] = max(f[i], f[j]+1);
            }
        }
        int res = 0;
        for(int i=0; i <n; i++) res = max(res, f[i]);
        return res;
    }
};

算法2 ：二分 + 贪心

2.1、算法思路

比如：在[4,10,8,4,3,9]中：
    长度为1： [4]
    长度为2： [4, 10] [4,8]
    长度为3： [3, 8, 9]
可以看得到长度为2的序列中，取[4,8]更好，这样当后面的数大于8，则长度就可以加1；
如果取[4,10]的时候，这样当后面的数小于10，如8的时候，就可以加进来了！！！

所以我们用一个数组f[i]表示长度为i的序列中的最后一位数字；然后枚举数组中的每一位数字x
if(x > f.back()) 加到f数组中
else{
找到f数组中第一个大于等于x的数y;
y = x;（这样就能保证最终f数组中的数是最小的）
}
最后输出f的长度就是最长上升子序列的长度了。

2.2、时间复杂度 O(n*logn)

2.3、C++ 代码

class Solution {
public:
    //时间为O(n*logn), 二分，贪心
    int lengthOfLIS(vector<int>& nums) {
        if(nums.empty()) return 0;
        vector<int> f;
        f.push_back(nums[0]); //长度为1的序列的末尾值为nums[0]
        for(int i = 1; i<nums.size(); i++)
        {
            if(nums[i] > f.back()) f.push_back(nums[i]);
            else{
                //然后在f[0]到f[i-1]中找到最后一个大于f[i]的，若没有则长度加1
                int l = 0, r = f.size()-1;
                while(l < r)
                {
                    int mid = (l + r) >>1;
                    if(f[mid] >= nums[i]) r = mid;
                    else l = mid + 1;
                }
                if(f[l] >= nums[i]) f[l] = nums[i];
            }

        }

        return f.size();
    }
};