题目描述

给你一个以 (radius, x_center, y_center) 表示的圆和一个与坐标轴平行的矩形 (x1, y1, x2, y2)，其中 (x1, y1) 是矩形左下角的坐标，(x2, y2) 是右上角的坐标。

如果圆和矩形有重叠的部分，请你返回 True，否则返回 False。

换句话说，请你检测是否 存在 点 (xi, yi)，它既在圆上也在矩形上（两者都包括点落在边界上的情况）。

样例

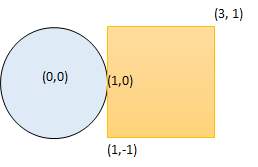
输入：radius = 1, x_center = 0, y_center = 0, x1 = 1, y1 = -1, x2 = 3, y2 = 1
输出：true
解释：圆和矩形有公共点 (1,0)

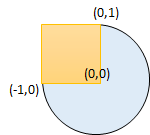
输入：radius = 1, x_center = 0, y_center = 0, x1 = -1, y1 = 0, x2 = 0, y2 = 1
输出：true

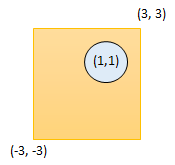
输入：radius = 1, x_center = 1, y_center = 1, x1 = -3, y1 = -3, x2 = 3, y2 = 3
输出：true

输入：radius = 1, x_center = 1, y_center = 1, x1 = 1, y1 = -3, x2 = 2, y2 = -1
输出：false

限制

• 1 <= radius <= 2000
• -10^4 <= x_center, y_center, x1, y1, x2, y2 <= 10^4
• x1 < x2
• y1 < y2

算法

(计算几何) $O(1)$

1. 先判定矩形的四个角是否在圆中。
2. 然后，如果圆心的横坐标在矩形横向的范围内，则我们 1) 看纵坐标是否在矩形纵向范围内（即圆心是否在矩形内）；2) 看纵坐标与矩形两个纵边的最短距离是否小于等于半径。
3. 如果圆心的纵坐标在矩形横向的范围内，则我们看横坐标与矩形的两个横边的最短距离是否小于等于半径。
4. 以上都不符合说明没有重叠。

时间复杂度

• 仅需要常数的时间。

空间复杂度

• 仅需要常数的额外空间。

C++ 代码

class Solution {
public:
    double sqr(int x) {
        return x * x;
    }

    bool check(int r, int x0, int y0, int x, int y) {
        return sqr(x0 - x) + sqr(y0 - y) <= sqr(r);
    }

    bool checkOverlap(int radius, int x_center, int y_center, int x1, int y1, int x2, int y2) {
        if (check(radius, x_center, y_center, x1, y1)
         || check(radius, x_center, y_center, x1, y2)
         || check(radius, x_center, y_center, x2, y1)
         || check(radius, x_center, y_center, x2, y2))
            return true;

        if (x1 <= x_center && x_center <= x2) {
            if (y1 <= y_center && y_center <= y2)
                return true;

            if (min(abs(y1 - y_center), abs(y2 - y_center)) <= radius)
                return true;
        }

        if (y1 <= y_center && y_center <= y2) {
            if (min(abs(x1 - x_center), abs(x2 - x_center)) <= radius)
                return true;
        }

        return false;
    }
};