题目

大家都知道 Fibonacci 数列吧，f1=1,f2=1,f3=2,f4=3,…,fn=fn−1+fn−2。
现在问题很简单，输入 n 和 m，求 fn 的前 n 项和 Snmodm。

输入格式
共一行，包含两个整数 n 和 m。

输出格式
输出前 n 项和 Snmodm 的值。

数据范围
1≤n≤2000000000,
1≤m≤1000000010
输入样例：
5 1000
输出样例：
12

题解

斐波那契数列是递归形式的，如果按递归来求解， 每一级都需要求两次加法【求解当前项和当前总和】，复杂度为O(N)，但是超时了！

假设斐波那契数列的第i项为：$[\begin{matrix} f_{i-1} & f_{i} & S_{i} \end{matrix}]$，则第$i-1$项和第$i$项的关系为：
$$ [\begin{matrix} f_{i-1} & f_{i} & S_{i} \end{matrix}]= [\begin{matrix} f_{i-2} & f_{i-1} & S_{i-1} \end{matrix}] \cdot\begin{bmatrix} 0 & 1 &1 \\ 1 &1 &1 \\ 0 &0 &1 \end{bmatrix} $$
则：

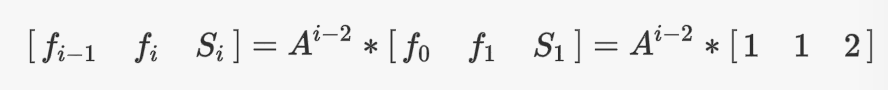
只需要用快速幂方法求出$A^{i-2}$即可，这样求解的复杂度只有O(logN)【求快速幂复杂度】。

代码

n,m = list(map(int,input().strip().split()))

start = [1,1,2]

# start * A**n-2

A = [[0,1,1],[1,1,1],[0,0,1]]

def Mul(A,B,m):
    # A,B 都是3*3的
    out = [[0]*3 for _ in range(3)]
    for i in range(3):
        for j in range(3):
            out[i][j] = A[i][0]*B[0][j]%m + A[i][1]*B[1][j]%m + A[i][2]*B[2][j]%m
    return out

def qmi(A,n,m):
    ans = [[1,0,0],[0,1,0],[0,0,1]]
    while n > 0:
        if n&1 : ans = Mul(ans,A,m)
        A = Mul(A,A,m)
        n = n>>1
    return ans

out = qmi(A,n-2,m)
ans = start[0]*out[0][2] + start[1]*out[1][2] + start[2]*out[2][2]
print(ans%m)