先附一张y总的讲课的板书~🙃

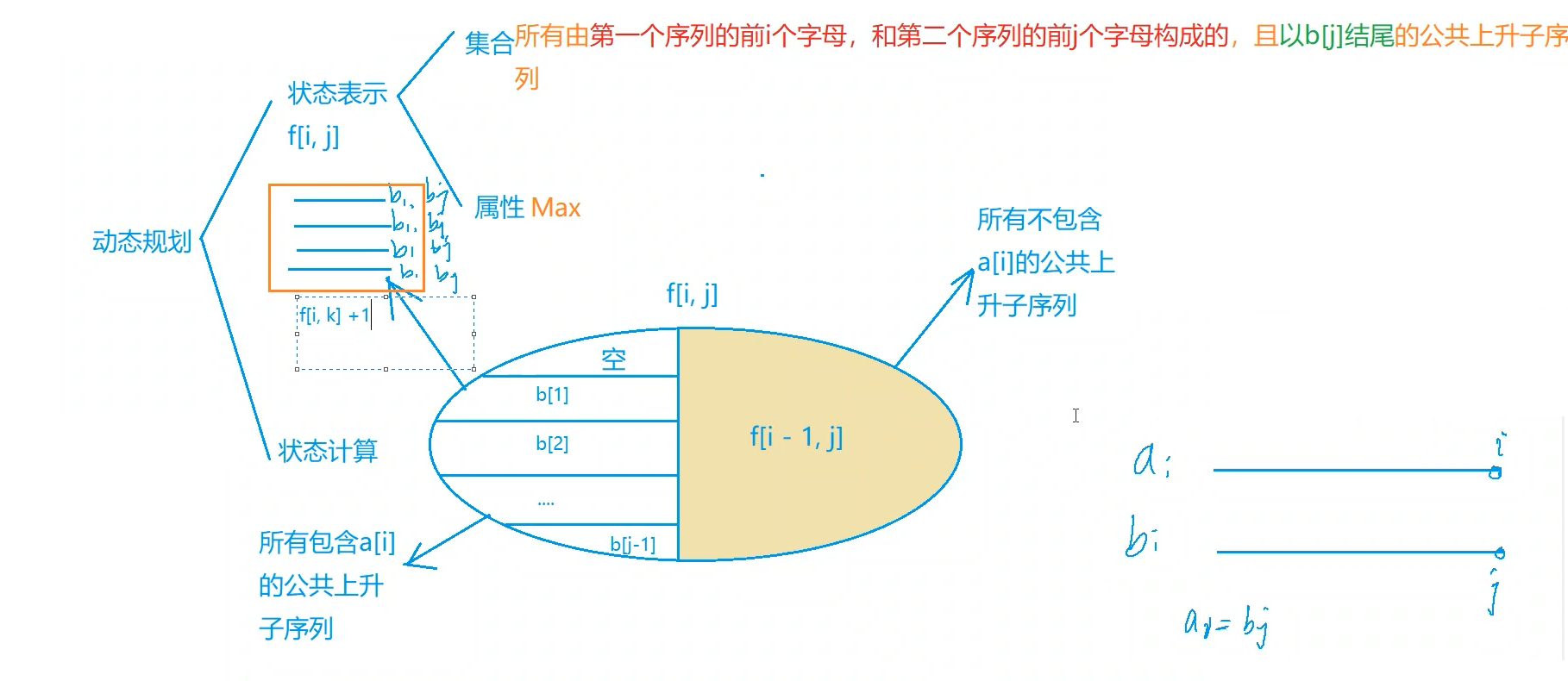
首先使朴素版的没有优化的做法

#include <iostream>
#include <cstdio>
using namespace std;
const int N = 3010;

int a[N], b[N], f[N][N];

int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i ++) scanf("%d", a + i);
    for (int j = 1; j <= n; j ++) scanf("%d", b + j);

    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= n; j ++)
        {
            f[i][j] = f[i - 1][j];
            if(a[i] == b[j]) // 当结尾相等的时候，才可能会有以下情况
                for (int k = 0; k < j; k ++)
                    if(b[k] < b[j]) // 判断b[k]是否可以是倒数第二个数
                        f[i][j] = max(f[i][j], f[i - 1][k] + 1);
        }

    int res = 0;
    for (int i = 1; i <= n; i ++) res = max(res, f[n][i]);

    printf("%d\n", res);

    return 0;
}

然后对代码进行等价变形

首先可以观察到第三重循环的进入条件是a[i]==b[j]，循环内部，是找到小于b[j]（也就是a[i]）的b[k]，然后来更新， 于是可以知道寻找的对象其实可以与j无关；
再看对象的寻找范围，由于k<j，所以可以在第二重循环外面记一个相对于第二重循环的全局最大值f[i][k] + 1,然后再循环的过程中，随着j的增长，来更新它；由此，可以省去k的循环（第三重）

代码如下：

#include <iostream>
#include <cstdio>
using namespace std;
const int N = 3010;

int a[N], b[N], f[N][N];

int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i ++) scanf("%d", a + i);
    for (int j = 1; j <= n; j ++) scanf("%d", b + j);

    for (int i = 1; i <= n; i ++)
    {
        int maxv = 1; // 当只有一个数的时候的长度
        for (int j = 1; j <= n; j ++)
        {
            f[i][j] = f[i - 1][j];
            if(a[i] == b[j]) f[i][j] = max(f[i][j], maxv); // 这里的maxv相当于k从1遍历到j-1的结果
            if(b[j] < a[i]) maxv = max(maxv, f[i - 1][j] + 1); // 更新maxv
        }
    }

    int res = 0;
    for (int i = 1; i <= n; i ++) res = max(res, f[n][i]);

    printf("%d\n", res);

    return 0;
}