题目描述

一个厨师收集了他 n 道菜的满意程度 satisfaction ，这个厨师做出每道菜的时间都是 1 单位时间。

一道菜的 「喜爱时间」系数定义为烹饪这道菜以及之前每道菜所花费的时间乘以这道菜的满意程度，也就是 time[i]*satisfaction[i] 。

请你返回做完所有菜 「喜爱时间」总和的最大值为多少。

你可以按 任意 顺序安排做菜的顺序，你也可以选择放弃做某些菜来获得更大的总和。

样例

输入：satisfaction = [-1,-8,0,5,-9]
输出：14
解释：去掉第二道和最后一道菜，最大的喜爱时间系数和为 (-1*1 + 0*2 + 5*3 = 14) 。
每道菜都需要花费 1 单位时间完成。

输入：satisfaction = [4,3,2]
输出：20
解释：按照原来顺序相反的时间做菜 (2*1 + 3*2 + 4*3 = 20)

输入：satisfaction = [-1,-4,-5]
输出：0
解释：大家都不喜欢这些菜，所以不做任何菜可以获得最大的喜爱时间系数。

输入：satisfaction = [-2,5,-1,0,3,-3]
输出：35

提示：

• n == satisfaction.length
• 1 <= n <= 500
• -10^3 <= satisfaction[i] <= 10^3

算法1

贪心 + 动态规划

先从小到大进行排序，菜的价值越大，炒得越多，收到的总价值就越大

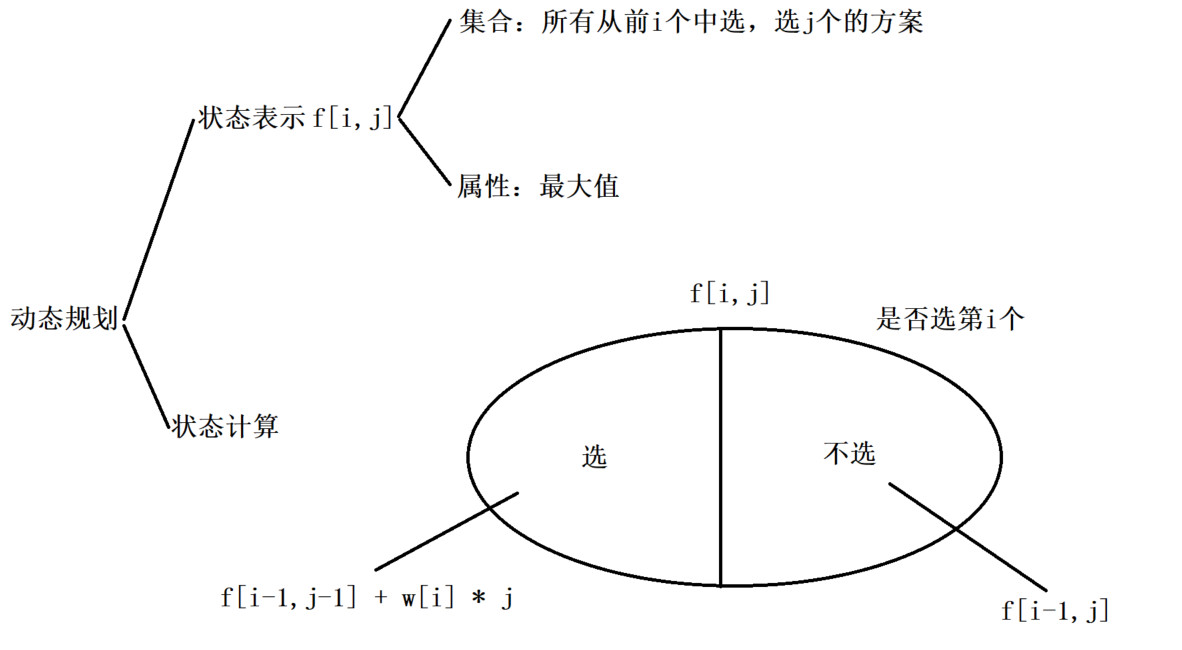
• 1、其中，为了方便处理，从前i个中选，选多少个必须得选，即使负数也无所谓，后面会判断，将f[][]数组全部赋值为负无穷，当j == 1的时候，表示从前i个中选1个，状态转移是f[i][j] = Math.max(f[i - 1][j],w[i])，即默认f[i - 1][j - 1]是等于0(这样处理可以让负数不参与干预)
• 2、从前i个中选，选择1个，2个，n个的所有情况中去最大值res，若res < 0表示最好的结果都是负数，返回0，否则返回res

时间复杂度$O(n^2)$

Java 代码

class Solution {
    static int N = 510;
    static int[][] f = new int[N][N];
    static int INF = 0x3f3f3f3f;
    public int maxSatisfaction(int[] satisfaction) {
        int n = satisfaction.length;
        Arrays.sort(satisfaction);
        int[] w = new int[N];
        for(int i = 1;i <= n;i ++) w[i] = satisfaction[i - 1];
        for(int i = 0;i <= n;i ++) Arrays.fill(f[i],-INF);
        for(int i = 1;i <= n;i ++)
        {
            for(int j = 1;j <= i;j ++)
            {
                if(j == 1) f[i][j] = Math.max(f[i - 1][j],w[i]);
                else f[i][j] = Math.max(f[i - 1][j],f[i - 1][j - 1] + w[i] * j);
            }
        }
        int res = 0;
        for(int i = 1;i <= n;i ++) res = Math.max(res,f[n][i]);

        if(res <= 0) return 0;
        return res;
    }
}

算法2

贪心

• 1、先从小到大进行排序，菜的价值越大，炒得越多，收到的总价值就越大
• 2、从后面一个一个加入，每新加一个数，之前加过的所有数sum都需要多加一遍，当之前加过的所有数sum < 0时，表示开始单调下降，因此当前位置是最大值

时间复杂度 $O(nlogn)$

Java 代码

class Solution {
    static int N = 510;
    static int[][] f = new int[N][N];
    static int INF = 0x3f3f3f3f;
    public int maxSatisfaction(int[] satisfaction) {
        int n = satisfaction.length;
        Arrays.sort(satisfaction);
        int sum = 0;
        int ans = 0;
        for(int i = n - 1;i >= 0;i --)
        {
            sum += satisfaction[i];
            if(sum < 0) break;
            ans += sum;
        }
        return ans;
    }
}