题目描述

你有一个 n x 3 的网格图 grid，你需要用 红，黄，绿 三种颜色之一给每一个格子上色，且确保相邻格子颜色不同（也就是有相同水平边或者垂直边的格子颜色不同）。

给你网格图的行数 n。

请你返回给 grid 涂色的方案数。由于答案可能会非常大，请你返回答案对 10^9 + 7 取余的结果。

样例

输入：n = 1
输出：12
解释：总共有 12 种可行的方法：

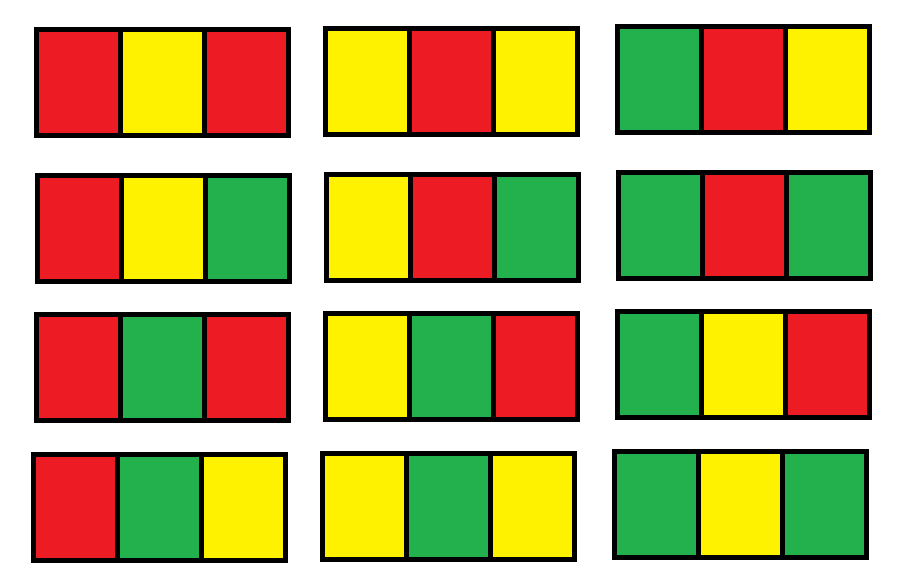
输入：n = 2
输出：54

输入：n = 3
输出：246

输入：n = 7
输出：106494

输入：n = 5000
输出：30228214

限制

• n == grid.length
• grid[i].length == 3
• 1 <= n <= 5000

算法

(状态压缩动态规划) $O(n)$

1. 首先预处理一行的 27 种情况，判断哪些情况是合法的。
2. 然后预处理两行之间的 27 * 27 种转移，判断哪些转移时合法的。
3. 设状态 $f(i, S)$ 表示填充了前 $i$ 行，其中第 $i$ 行的填充方式是 $S$ 的方案数。这里的 $S$ 是一个三位三进制的数字，例如 $(010)_3$ 可以表示第一个位置填红色，第二个位置填黄色，第三个位置填红色。
4. 初始时，对于合法的 $S$，$f(0, S) = 1$。其余为 0。
5. 转移时，枚举 $S_j$ 和 $S_k$，如果 $S_j$ 和 $S_k$ 都合法且 $S_j$ 和 $S_k$ 作为先后两行也合法，则转移 $f(i, k) = f(i, k) + f(i - 1, j)$。
6. 最终答案为，对于所有合法的 $S$，$\sum_S f(n - 1, S)$

时间复杂度

• 预处理的时间为常数。
• 动态规划的状态数为 $O(n)$，转移的时间为常数，故总时间复杂度为 $O(n)$。

空间复杂度

• 需要额外 $O(n)$ 的空间记录状态。
• 可以通过滚动优化到常数。

C++ 代码

class Solution {
public:
    bool check_row(int x) {
        vector<int> a(3);
        for (int i = 0; i < 3; i++) {
            a[i] = x % 3;
            x /= 3;
        }

        for (int i = 0; i < 2; i++)
            if (a[i] == a[i + 1])
                return false;

        return true;
    }

    bool check(int x, int y) {
        vector<int> a(3), b(3);
        for (int i = 0; i < 3; i++) {
            a[i] = x % 3;
            x /= 3;
            b[i] = y % 3;
            y /= 3;
        }

        for (int i = 0; i < 3; i++)
            if (a[i] == b[i])
                return false;

        return true;
    }

    int numOfWays(int n) {
        const int mod = 1000000007;
        vector<bool> v(27);
        vector<vector<bool>> t(27, vector<bool>(27, false));
        for (int i = 0; i < 27; i++)
            v[i] = check_row(i);

        for (int i = 0; i < 27; i++)
            if (v[i])
                for (int j = 0; j < 27; j++)
                    if (v[j])
                        t[i][j] = check(i, j);

        vector<vector<int>> f(n, vector<int>(27, 0));

        for (int j = 0; j < 27; j++)
            f[0][j] = v[j];

        for (int i = 1; i < n; i++)
            for (int j = 0; j < 27; j++)
                if (v[j])
                    for (int k = 0; k < 27; k++)
                        if (v[k] && t[j][k])
                            f[i][k] = (f[i][k] + f[i - 1][j]) % mod;

        int ans = 0;
        for (int j = 0; j < 27; j++)
            ans = (ans + f[n - 1][j]) % mod;

        return ans;
    }
};