题目描述

You have a grid of size n x 3 and you want to paint each cell of the grid with exactly one of the three colours: Red, Yellow or Green while making sure that no two adjacent cells have the same colour (i.e no two cells that share vertical or horizontal sides have the same colour).

You are given n the number of rows of the grid.

Return the number of ways you can paint this grid. As the answer may grow large, the answer must be computed modulo 10^9 + 7.

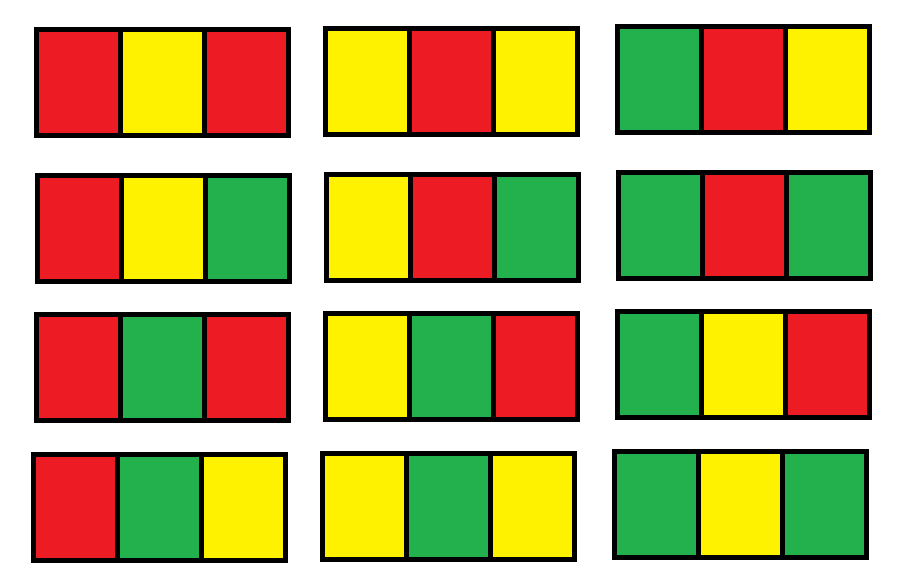
样例

Example 1:

Input: n = 1
Output: 12
Explanation: There are 12 possible way to paint the grid as shown:

Example 2:

Input: n = 2
Output: 54

Example 3:

Input: n = 3
Output: 246

Example 4:

Input: n = 7
Output: 106494

Example 5:

Input: n = 5000
Output: 30228214

Constraints:

• n == grid.length
• grid[i].length == 3
• 1 <= n <= 5000

算法

时间复杂度 $O(n)$

空间复杂度 $O(1)$

假设三种颜色用ABC分别表示，那么当n = 1的时候，有3 * 2 * 2 = 12种，当n = 2的时候，前一种的排列方式会对后面产生影响，仅仅以假设第一行的前两个染色为AB，考察后面的染色：

如果第一行最后一个和第一行第一个同色，即ABA
那么第二行可能的染色方案是：
BAB BAC CAB CAC BCB

如果第一行最后一个的染色和第一行第一个不是同色，
那么第二行可能的染色方案是：
BCA BCB BAB CAB

这时候发现规律，如果第二行出现BAB，那么和第一行出现ABA所得结果种类是一样的，于是发现，n+1的染色方案和第n行最后一个和第n行第一个染色是否同色有关，于是找到规律，每一个同色的方案会产生5种方案，其中3种同色方案和2种不同色方案；每一个不同色方案会产生2种同色方案和2种非同色方案。

经过上面的分析，发现只需要维护每一行同色的方案数量和不同色的方案数量，分别用变量equal和notEqual来维护，则n + 1的方案数是equal * 5 + notEqual * 4，记得更新equal和notEqual的数值，以及可能产生的溢出问题。

另外以染色为背景的题目还有：

• HDU 2045 不容易系列之(3)—— LELE的RPG难题（染色类型问题）
• UVA 11916 - Emoogle Grid（虽然是染色背景，但是考察的是数论）可以和前面两个染色问题关联起来思考。

C++ 代码

class Solution {
public:
    int numOfWays(int n) {
        std::ios_base::sync_with_stdio(false);
        cin.tie(NULL);
        cout.tie(NULL);

        const long long MODE = 1e9 + 7;

        long long equal = 6, notEqual = 6;
        if (n == 1) return 12;
        long long res;
        for (int i = 2; i <= n; ++i) {
            res = (equal * 5 % MODE + notEqual * 4 % MODE) % MODE;
            long long a = equal, b = notEqual;
            equal = (a * 3 % MODE + b * 2 % MODE) % MODE;
            notEqual = (a * 2 % MODE + b * 2 % MODE) % MODE;
        }

        return res;
    }
};