题意

K 个鸡蛋，并可以使用一栋从 1到 N 共有 N 层楼的建筑。
鸡蛋的硬度为F，满足 0 <= F <= N ，相对应的 从F楼层或比它低的楼层落下的鸡蛋都不会破。
每次移动，你可以取一个鸡蛋（如果你有完整的鸡蛋）并把它从任一楼层 X 扔下（满足 1 <= X <= N）。
你的目标是确切地知道 F 的值是多少。
无论 F 的初始值如何，你确定 F 的值的最小移动次数是多少

样例

输入样例：

100 1
100 2

输出样例：

100
14

样例解释

如果只有一个鸡蛋，你只能从第一层开始扔，在最坏的情况下，鸡蛋的硬度是100，所以需要扔100次。如果采用其他策略，你可能无法测出鸡蛋的硬度(比如你第一次在第二层的地方扔,结果碎了,这时你不能确定硬度是0还是1)，即在最坏情况下你需要扔无限次，所以第一组数据的答案是100。

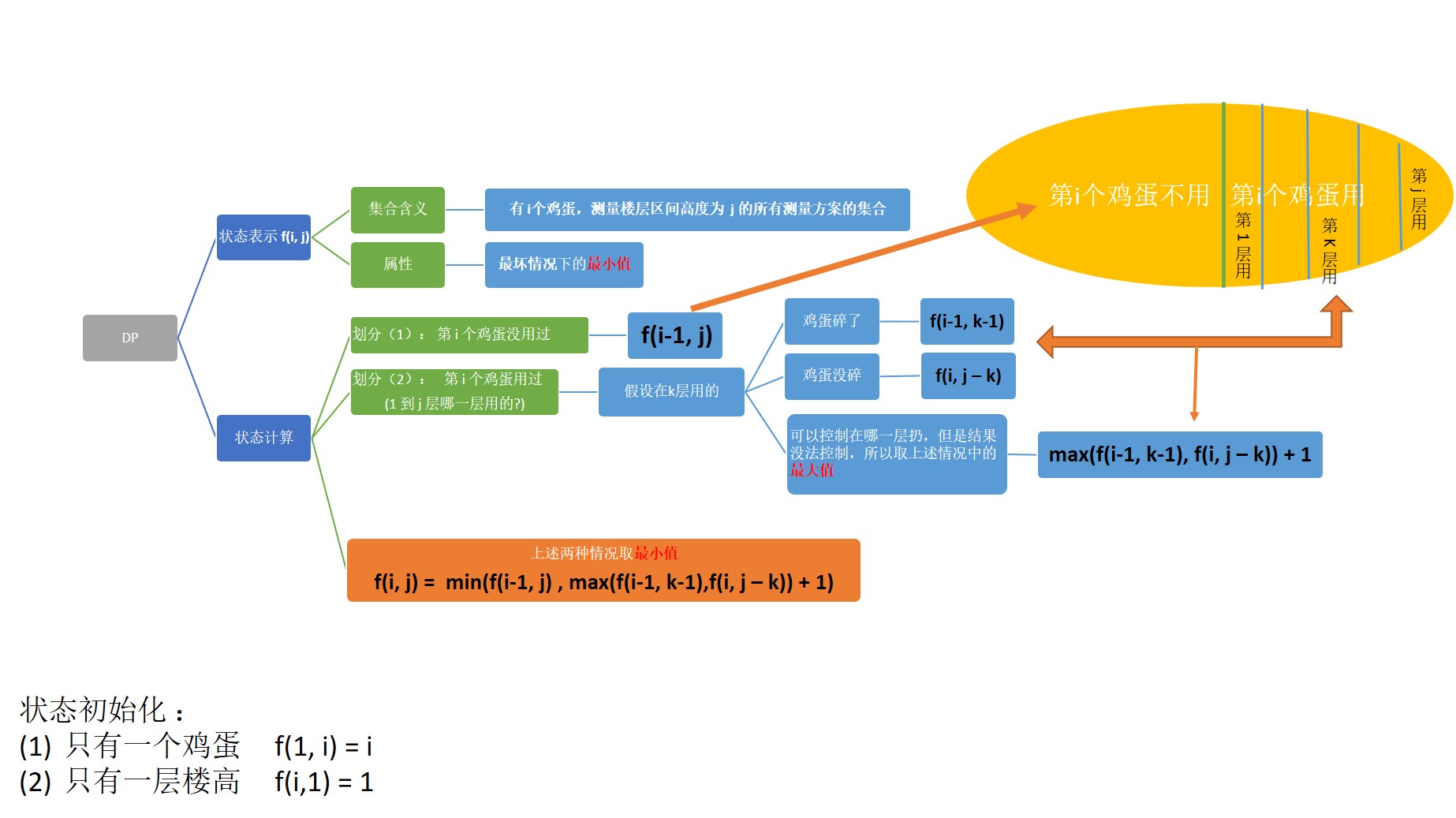
算法（动态规划） $o(nm^2)$ (n鸡蛋个数，m楼层高度)

c++ 代码

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 11, M = 110;

int n, m; // n个鸡蛋 m层楼
int f[N][M];

int main()
{
    while (cin >> m >> n)
    {
         // 根据集合含义状态初始化 
         //只有一个鸡蛋,i层楼最坏情况下的最少丢鸡蛋次数都为i
        for (int i = 1; i <= m; i ++ ) f[1][i] = i;
         //无论多少个鸡蛋,在只有一层楼的情况下最坏情况下的最少丢鸡蛋次数都为1
        for (int i = 1; i <= n; i ++ ) f[i][1] = 1;  

        for (int i = 2; i <= n; i ++ )
            for (int j = 2; j <= m; j ++ )
            {
                f[i][j] = f[i - 1][j];
                for (int k = 1; k <= j; k ++ )
                    f[i][j] = min(f[i][j], max(f[i - 1][k - 1], f[i][j - k]) + 1);
            }

        cout << f[n][m] << endl;
    }

    return 0;
}

思考拓展

• 空间复杂度 ：能否用一位滚动数组
• 时间复杂度 ：max(f[i - 1][k - 1], f[i][j - k]) 前者随着k递增，后者随着k递减 ，能够优化到$0(nm)$ ??