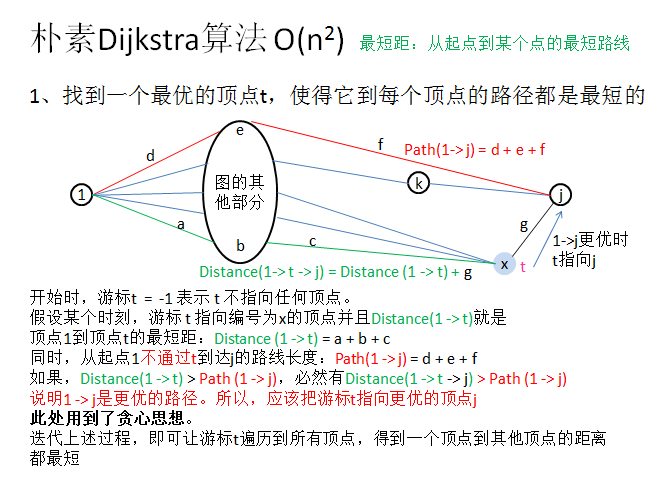
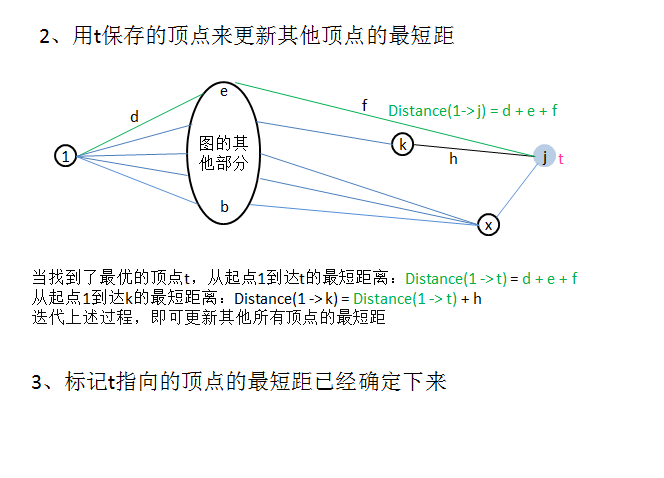
算法

时间复杂度 $O(n^2)$

C++ 代码

#include <iostream>
#include <cstring>
using namespace std;
// 最大规模，正无穷，字节填充
const int N = 510, inf = 0x3f3f3f3f, stuff = 0x3f;
int n, m, a, b, c; // 顶点数，有向边数，a和b是相邻的两个顶点的编号，边a->b的长度
// 稠密图用邻接矩阵来表示，从起点到某顶点的最短距，标记已确定了最短距的顶点
int g[N][N], d[N], st[N]; 

int dijkstra() {
    memset(d, stuff, sizeof d); // 初始化最短距数组
    d[0] = 0; // 起点的最短距为0
    for(int i = 0; i < n; i++) { 
        int t = -1; // t是游标，初始化成-1，表示t不指向任何顶点，d[t]是确定的最短距
        for(int j = 0; j < n; j++) {    // 从顶点0开始，d[0]是最短距已确定
            // (a)顶点j的最短距已经确定
            // (b)游标t确实指向一个顶点(t != -1，保证在数组d中不下越界)
            //    从起点到达t的最短距小于从起点不经过t到达j的路径
            if(st[j] || (~t && d[t] < d[j])) continue; // 跳过这样的顶点
            t = j; // 游标t指向顶点j
        }
        // 用t的最短距更新其他所有顶点的最短距
        // (从起点到达t的路径 + t到k的边长)的长度与
        // 从起点不经过t到达k的路径取最小者，即为k的最短距
        for(int k = 0; k < n; k++) 
            d[k] = min(d[t] + g[t][k], d[k]);
        st[t] = 1; // 标记t指向的顶点的最短距已经确定
    }
    if(d[n - 1] == inf) return -1; // 起点到顶点n-1的最短距不存在，返回-1
    return d[n - 1]; // 存在返回这个最短距        
}

int main() {
    memset(g, stuff, sizeof g); // 初始化邻接矩阵
    cin >> n >> m; // 读入顶点数以及边数
    while(m--) {   // 根据边数录入相邻的一组顶点以及它们之间的边
        cin >> a >> b >> c;
        a--, b--;  // 顶点减一，算法为了以后能符合STL从0开始的惯例
        g[a][b] = min(g[a][b], c); // g[a][b]是a到b的边长，c亦是，取最小者为边
    }
    cout << dijkstra();
    return 0;
}