题目描述

给定一棵包含 N 个节点的完全二叉树，树上每个节点都有一个权值，按从上到下、从左到右的顺序依次是 A1,A2,⋅⋅⋅AN，如下图所示：
现在小明要把相同深度的节点的权值加在一起，他想知道哪个深度的节点权值之和最大？
如果有多个深度的权值和同为最大，请你输出其中最小的深度。
注：根的深度是 1。
输入格式
第一行包含一个整数 N。
第二行包含 N 个整数 A1,A2,⋅⋅⋅AN。
输出格式
输出一个整数代表答案。
数据范围
1≤N≤105,
−10^5≤Ai≤10^5

样例

7
1 6 5 4 3 2 1

2

算法1

(递推)

首先因为是完全二叉树因此，故而联想到堆,堆同样是一个完全二叉树在y总算法基础课中，
使用了数组模拟完全二叉树。其过程如下。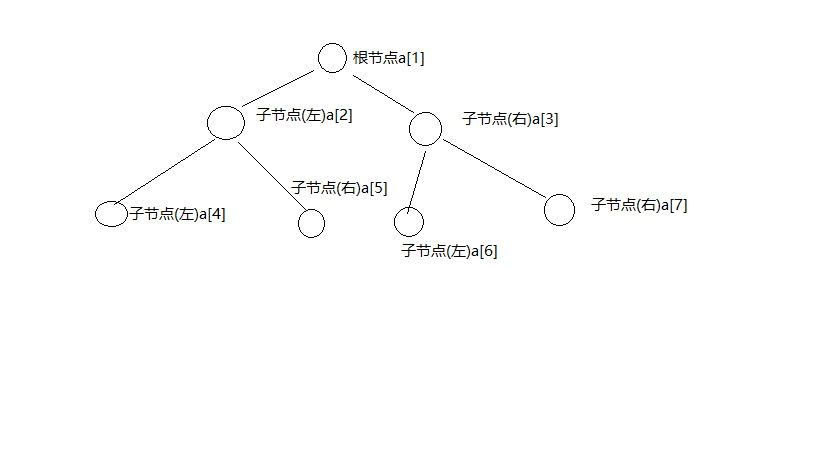

通过该图可知，对于完全而叉树的非最后一层，在使用数组模拟中均满足
在当前层数的最左端节点的下标的两倍
等于下一层中最左端节点的下标，
在当前层数的最右端节点的下标的两倍加一
等于下一层中最右端节点的下标。
故可以使用递推的方式，得到二叉树每一层的最左端节点和最右端节点，的下标
使用循环限制二叉树每一层在数组中的左右两端的下标。
找到每一层所在数组的区间，并计算区间和，找到和最大的层数。

C++ 代码

#include<iostream>
using namespace std;
const int N=100010;
long long a[N];
long long Max=-1e18,res=1;
void dfs(int left,int right,int n,int deepin)
{
    long long alls=0;
    int i;
    for(i=left;i<=right&&i<=n;i++)alls+=a[i];
    if(alls>Max)Max=alls,res=deepin;
    if(i>=n+1)return;
    dfs(left*2,right*2+1,n,deepin+1);
}
int main()
{
    long long n;
    cin>>n;
    for(int i=1;i<=n;i++)cin>>a[i];
    dfs(1,1,n,1);
    cout<<res<<endl;
    return 0;
}

如有错误，欢迎指正，萌新一枚第一次写题解，图不好看请见谅。