题目描述

直方图是由在公共基线处对齐的一系列矩形组成的多边形。

矩形具有相等的宽度，但可以具有不同的高度。

例如，图例左侧显示了由高度为2,1,4,5,1,3,3的矩形组成的直方图，矩形的宽度都为1：

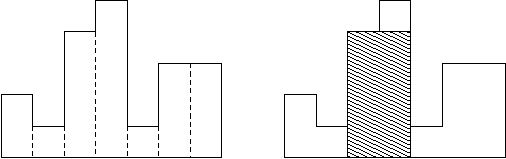
通常，直方图用于表示离散分布，例如，文本中字符的频率。

现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

图例右图显示了所描绘直方图的最大对齐矩形。

输入格式
输入包含几个测试用例。

每个测试用例占据一行，用以描述一个直方图，并以整数n开始，表示组成直方图的矩形数目。

然后跟随n个整数h1，…，hn。

这些数字以从左到右的顺序表示直方图的各个矩形的高度。

每个矩形的宽度为1。

同行数字用空格隔开。

当输入用例为n=0时，结束输入，且该用例不用考虑。

输出格式
对于每一个测试用例，输出一个整数，代表指定直方图中最大矩形的区域面积。

每个数据占一行。

请注意，此矩形必须在公共基线处对齐。

数据范围
1≤n≤100000,
0≤hi≤1000000000

样例

输入样例：
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
输出样例：
8
4000

(单调栈) $O(n)$

问题可以转换为遍历数组nums，对数组中每一个元素s，求该元素往左看第一个小于它的元素的坐标，往右看第一个小于它的元素的坐标。

方法是单调栈，对nums遍历，对其中的每一个元素s，根据不同问题入栈s对应下标或s，每次对比s与栈顶元素top（或其对应s）比较,当栈非空且top大于等于s时出栈，此时栈非空，那么栈顶肯定为往左看第一个小于当前s的元素，对于s后续待遍历的元素ss，发现若s<ss，s便是结果，若s>=ss，那么把s出栈，之前计算s的时候出栈的元素都大于s，所以不用管了，继续往后看便是;若栈为空,说明s左边的元素都大于等于s，此时记录遍历结果的数组left记录比最左边元素下标小于1，这样后续得出右边看的下标，再去计算差值才是对的，比如：

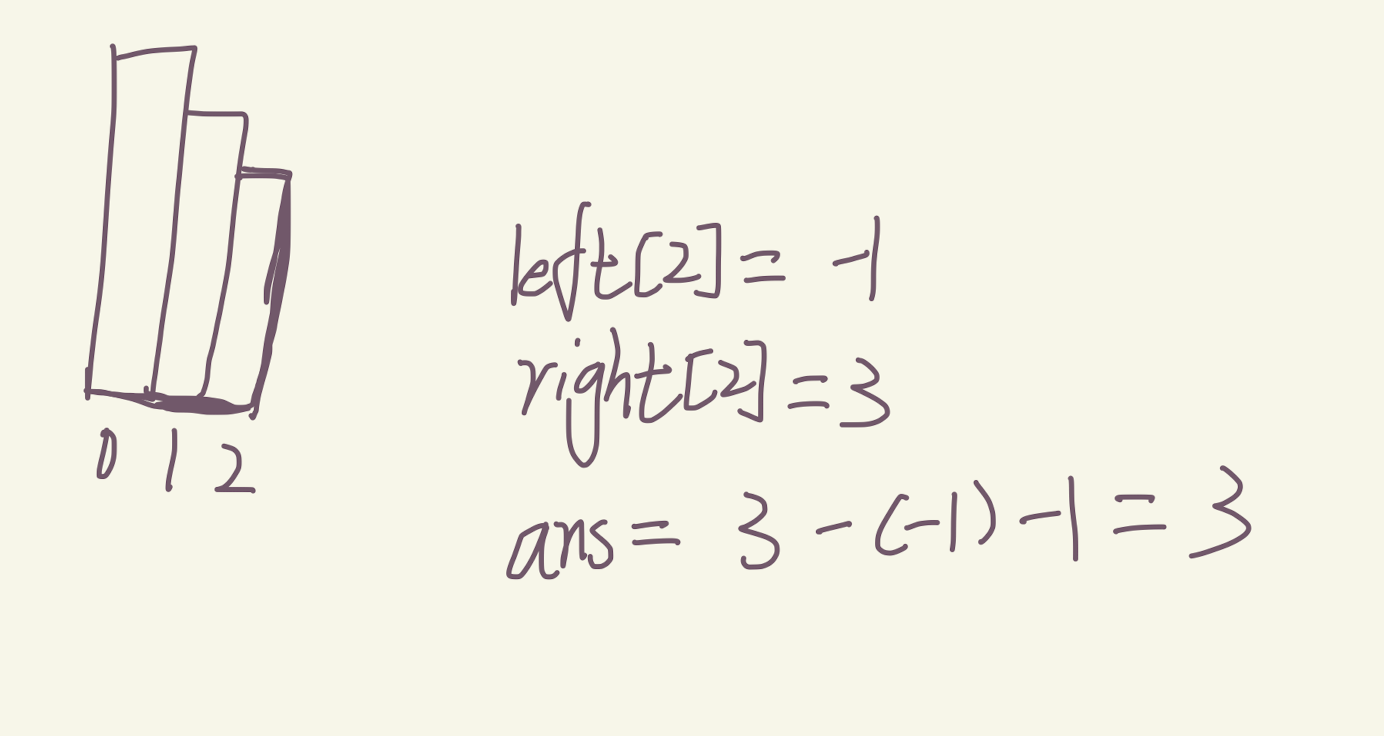
nums:  7  2  1  4  5  1  3  3

index: 0  1  2  3  4  5  6  7

h:    -1 -1 -1  2  3  -1  5  5

从后往前遍历得到往右看的结果，不过坐标要注意变换下。

时间复杂度

python 代码

if __name__ == "__main__":
    while True:
        nums = list(map(int, input().split()))
        n = nums[0]
        nums = nums[1:]
        if n == 0: break
        lt, rt = [], []
        st = []
        for idx, num in enumerate(nums):
            while st and nums[st[-1]] >= num:
                st.pop()
            if not st:
                lt.append(-1) 
            else:
                lt.append(st[-1])
            st.append(idx)

        st.clear()
        for idx in range(len(nums) - 1, -1, -1):
            while st and nums[st[-1]] >= nums[idx]:
                st.pop()
            if not st:
                rt.append(n)
            else:
                rt.append(st[-1])
            st.append(idx)

        res = 0
        for i in range(n):
            res = max(res, nums[i] * (rt[n - i - 1] - lt[i] - 1))
        print(res)