题目描述

给出一棵 $n$ 个点的数，然后进行 $m$ 次询问
每次给出三个点 $a, b, c$ 求到三个点的距离之和最小的点，和最小的距离之和

倍增求lca

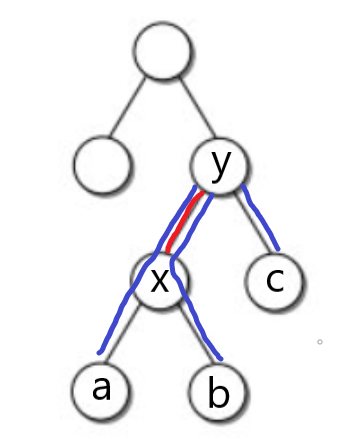
以上图为例，我们发现三个点两两求lca，必定有两个lca是重复的 $lca(a, c) = y$ , $lca(b, c) = y$

换一种说法，对于任意的三个点 $a, b, c$，必定存在一个点 $y$，使得 $lca(a, c) = y$ 且 $lca(b, c) = y$
(以上图为例，a, b, c可交换)

同时，必定存在一个点 $x$ 使得它到三个点的路径没有重叠部分。

发现了这些性质这个题就比较显然了
$x$ 就是两个lca中深度较深的那个，求出三个点到它的距离之和即可，距离之和等于蓝边之和减去红边

时间复杂度 $O(mlogn)$

C++ 代码

#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 5e5 + 10, M = N * 2;

int h[N], e[M], ne[M], idx;
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

int n, m;
int dep[N], f[N][20];
void dfs(int u, int fa)
{
    dep[u] = dep[fa] + 1, f[u][0] = fa;
    for(int i = 1; i < 20; i ++)  f[u][i] = f[f[u][i - 1]][i - 1];

    for(int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if(j == fa)  continue;
        dfs(j, u);
    }
}

int lca(int a, int b)
{
    if(dep[a] < dep[b])  swap(a, b);

    for(int i = 19; i >= 0; i --)
        if(dep[f[a][i]] >= dep[b])
            a = f[a][i];

    if(a == b)  return a;

    for(int i = 19; i >= 0; i --)
        if(f[a][i] != f[b][i])
            a = f[a][i], b = f[b][i];
    return f[a][0];
}

int main()
{
    memset(h, -1, sizeof h);
    scanf("%d%d", &n, &m);
    for(int i = 1; i < n; i ++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);
    }

    dfs(1, 0);

    while(m --)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);

        int x = lca(a, b), y = lca(a, c), z = lca(b, c);

        if(x == y)  swap(y, z);             //  让z成为那个重复的
        if(dep[x] < dep[y])  swap(x, y);    //  让x成为深度较大的

        int sum = dep[a] + dep[b] + dep[c] - dep[y] * 3 - (dep[x] - dep[y]);
        printf("%d %d\n", x, sum);
    }
    return 0;
}