题目描述

输入一个奇数n，输出一个由‘*’构成的n阶实心菱形。

算法

到中心单元的曼哈顿距离

在二维空间中 $i,j$ 两点的曼哈顿距离可以表示为 $d(i,j)=|xi-xj|+|yi-yj|$ （横、纵坐标差值的绝对值之和）。

此题目可认为是使得到中心单元的曼哈顿距离满足一定条件即打印星号。

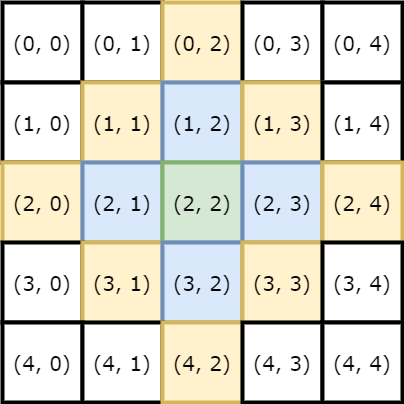
上图示例输入为 $n=5$ 时的情况，使用不同颜色区分各单元到中心单元的曼哈顿距离。输入奇数 $n$，坐标 $(n/2, n/2)$ 表示 $n*n$ 方阵中的中心单元。

对于满足题目条件的任意菱形，总是会出现相似的结构。菱形即为与此 $n*n$ 方阵中心的曼哈顿距离不超过 $n/2$ 的所有单元的集合。

因此，打印‘*’的判断条件是 $abs(i - n/2) + abs(j - n/2) <= n/2$。

C++ 代码

#include <iostream>
using namespace std;

int main()
{
    int n;
    scanf("%d", &n);
    for(int i=0;i<n;++i)
    {
        for(int j=0;j<n;++j)
        {
            if(abs(i-n/2)+abs(j-n/2)<=n/2) printf("*");
            else printf(" ");
        }
        puts("");
    }

    return 0;
}