题目描述

某个程序本来应该输出一个整数数组。但是这个程序忘记输出空格了以致输出了一个数字字符串，我们所知道的信息只有：数组中所有整数都在 [1, k] 之间，且数组中的数字都没有前导 0 。

给你字符串 s 和整数 k 。可能会有多种不同的数组恢复结果。

按照上述程序，请你返回所有可能输出字符串 s 的数组方案数。

由于数组方案数可能会很大，请你返回它对 10^9 + 7 取余 后的结果。

样例

输入：s = "1000", k = 10000
输出：1
解释：唯一一种可能的数组方案是 [1000]

输入：s = "1000", k = 10
输出：0
解释：不存在任何数组方案满足所有整数都 >= 1 且 <= 10 同时输出结果为 s 。

输入：s = "1317", k = 2000
输出：8
解释：可行的数组方案为 [1317]，[131,7]，[13,17]，[1,317]，[13,1,7]，[1,31,7]，[1,3,17]，[1,3,1,7]

输入：s = "2020", k = 30
输出：1
解释：唯一可能的数组方案是 [20,20] 。 [2020] 不是可行的数组方案，
原因是 2020 > 30 。 [2,020] 也不是可行的数组方案，因为 020 含有前导 0 。

输入：s = "1234567890", k = 90
输出：34

提示：

• 1 <= s.length <= 10^5.
• s 只包含数字且不包含前导 0 。
• 1 <= k <= 10^9.

算法分析

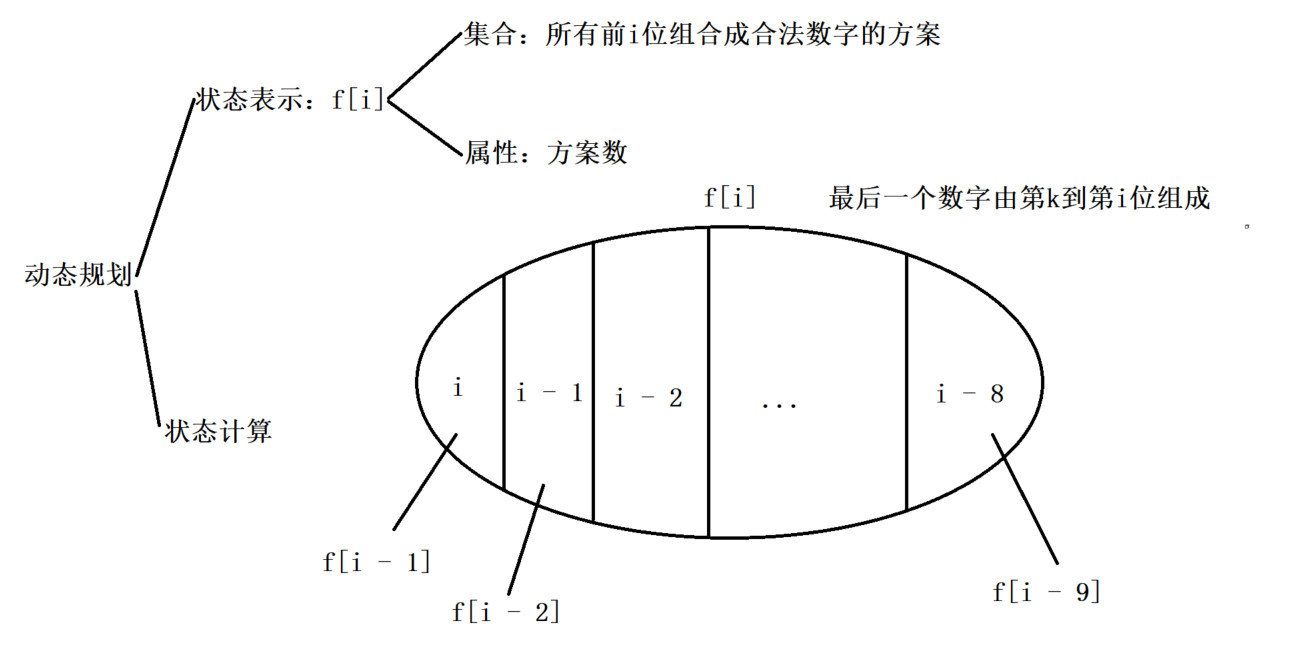
注意：需要判断最后一个数字是否合法，若合法则包括该情况

时间复杂度 $O(10 * n)$

Java 代码

class Solution {
    static int N = 100010;
    static int mod = 1000000000 + 7;
    static long[] f = new long[N];
    public int numberOfArrays(String s, int k) {
        int n = s.length();
        s = " " + s;
        char[] g = s.toCharArray();
        Arrays.fill(f,0);
        f[0] = 1;
        for(int i = 1;i <= n;i ++)
        {
            long t = 0;
            int cnt = 1;
            for(int j = i;j > 0 && j > i - 9;j --)
            {
                t = t + (g[j] - '0') * cnt;
                cnt *= 10;
                if(g[j] == '0') continue;
                if(t > 0 && t <= k)  f[i] = (f[i] + f[j - 1]) % mod;

            }
        }
        return (int)f[n];
    }
}