题目描述

给你三个整数 n、m 和 k 。下图描述的算法用于找出正整数数组中最大的元素。

请你生成一个具有下述属性的数组 arr ：

• arr 中有 n 个整数。
• 1 <= arr[i] <= m 其中 (0 <= i < n) 。
• 将上面提到的算法应用于 arr ，search_cost 的值等于 k 。

返回上述条件下生成数组 arr 的 方法数 ，由于答案可能会很大，所以 必须 对 10^9 + 7 取余。

样例

输入：n = 2, m = 3, k = 1
输出：6
解释：可能的数组分别为 [1, 1], [2, 1], [2, 2], [3, 1], [3, 2] [3, 3]

输入：n = 5, m = 2, k = 3
输出：0
解释：没有数组可以满足上述条件

输入：n = 9, m = 1, k = 1
输出：1
解释：可能的数组只有 [1, 1, 1, 1, 1, 1, 1, 1, 1]

输入：n = 50, m = 100, k = 25
输出：34549172
解释：不要忘了对 1000000007 取余

输入：n = 37, m = 17, k = 7
输出：418930126

提示：

• 1 <= n <= 50
• 1 <= m <= 100
• 0 <= k <= n

算法分析

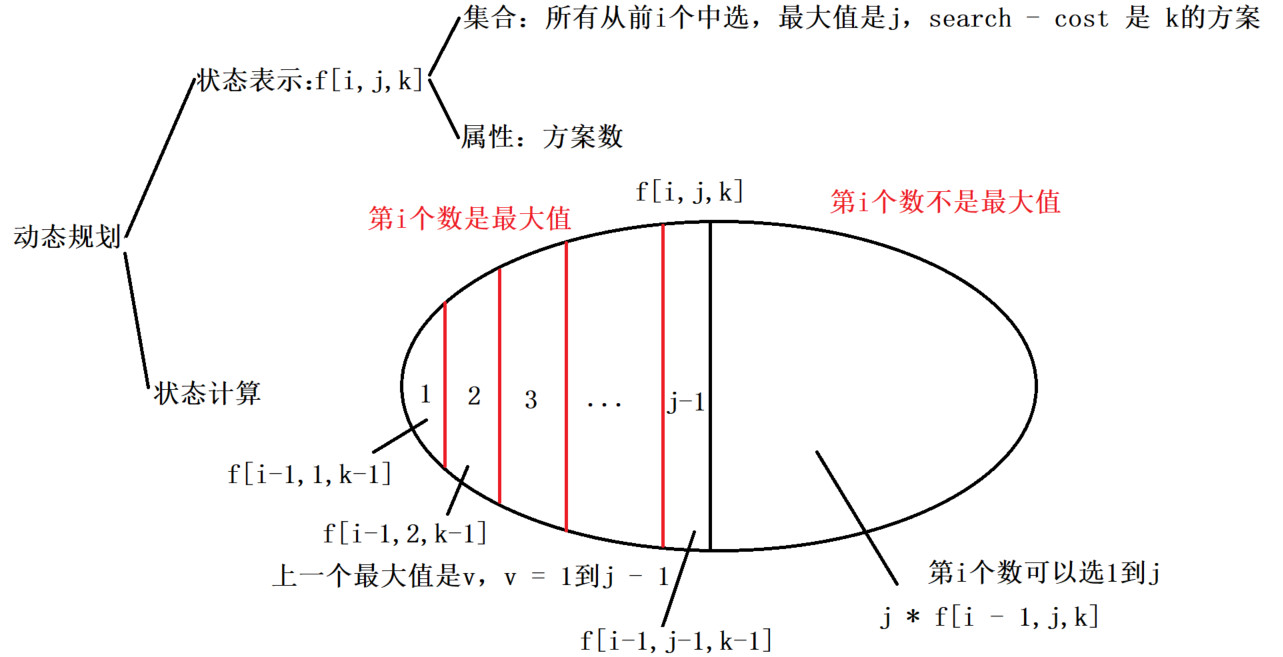
初始化f[1][i][1] = 1,i从1到m

时间复杂度 $O(nm^2k)$

Java代码

class Solution {
    static int mod = 1000000000 + 7;
    static long[][][] f = new long[55][110][55];
    public int numOfArrays(int n, int m, int k) {
        for(int i = 0;i <= n;i ++)
            for(int j = 0;j <= m;j ++)
                Arrays.fill(f[i][j],0);

        for(int i = 1;i <= m;i ++) f[1][i][1] = 1;

        for(int i = 1;i <= n;i ++)
            for(int j = 1;j <= m;j ++)
                for(int s = 1;s <= k;s ++)
                {
                    f[i][j][s] = (f[i][j][s] + j * f[i - 1][j][s]) % mod;
                    for(int v = 1;v < j;v ++)
                    {
                        f[i][j][s] = (f[i][j][s] + f[i - 1][v][s - 1]) % mod;
                    }
                }

        long res = 0;
        for(int i = 1; i <= m;i ++) res = (res + f[n][i][k]) % mod;
        return (int)res;
    }
}