算法分析

设$(x_0,y_0)$是某一直线射到的点，则该方程为$y = \frac{y_0}{x_0}x$，在该直线上的其他点均是$(x_0,y_0)$的倍数，即$(mx_0,my_0)$，因此$(x_0,y_0)$具有互质的性质

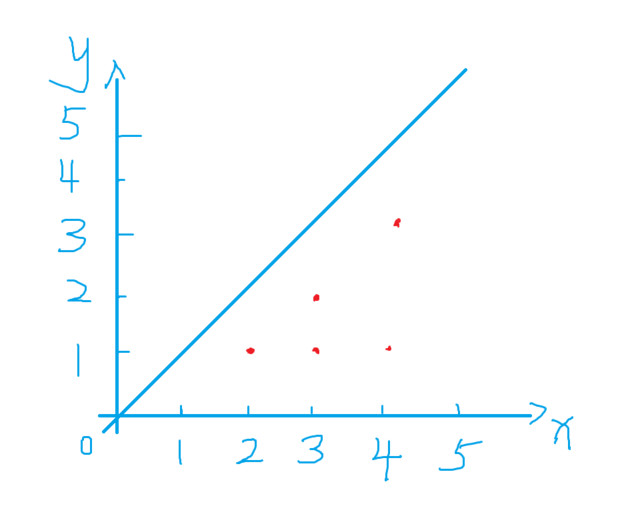
由于欧拉函数求的是1 ~ N 中与 N 互质的数的个数，若需要联系到欧拉函数，与n互质的数需要小于等于它本身，因此求0 <= x ,y <= N中，(x,y)互质的个数需要进行分类，使得某一边小于等于另一边，如图所示，对y = x直线进行切割，使得两边的点对称，只需求右下方区域即可，右下区域的点满足x > y的性质，且y 属于1到x - 1的区间，因此对于每个x，求出1到x - 1中与x互质的数的个数，即相当于求x的欧拉函数,因此用筛法求出1到x的所有欧拉函数

由于2到n中的欧拉函数的个数需要算两次，而x = 1时只需要算一次，因此$res = ph(1) + \sum_{i = 2}^{n}ph(i)$

时间复杂度 $O(n)$

参考文献

算法提高课

Java 代码

import java.util.Scanner;

public class Main {
    static int N = 1010;
    static int[] primes = new int[N];
    static boolean[] st = new boolean[N];
    static int cnt = 0;
    static int[] phi = new int[N];
    static void init(int n)
    {
        phi[1] = 1;
        for(int i = 2;i <= n;i ++)
        {
            if(!st[i])
            {
                primes[cnt ++] = i;
                phi[i] = i - 1;
            }
            for(int j = 0;primes[j] * i <= n;j ++)
            {
                st[primes[j] * i] = true;
                if(i % primes[j] == 0) 
                {
                    phi[primes[j] * i] = primes[j] * phi[i];
                    break;
                }
                phi[primes[j] * i] = (primes[j] - 1) * phi[i];
            }
        }
    }
    public static void main(String[] args)  {
       Scanner scan = new Scanner(System.in);
       int T = scan.nextInt();
       init(1000);
       for(int i = 1;i <= T;i ++)
       {
           int n = scan.nextInt();
           //注意(1, 0)和(0, 1)是特殊点，并不是满足欧拉函数的点，
           //(1, 1)是欧拉函数的点，欧拉函数是1到N互质的数的个数，
           int res = 1;
           for(int j = 1;j <= n;j ++) res += phi[j] * 2;
           System.out.println(i + " " + n + " " + res);
       }
    }
}

gcd会超时

import java.util.HashSet;
import java.util.Scanner;

public class Main {
    static HashSet<String> set = new HashSet<String>();
    static int gcd(int a, int b)
    {
        return b == 0 ? a : gcd(b, a % b);
    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int T = scan.nextInt();
        for(int u = 1;u <= T;u ++)
        {
            set.clear();
            int n = scan.nextInt();
            for(int i = 0;i <= n;i ++)
                for(int j = 0;j <= n;j ++)
                {
                    if(i == 0 && j == 0) continue;
                    int a = i, b = j;
                    int t = gcd(a, b);
                    a /= t;
                    b /= t;
                    String s = a + "#" + b;
                    if(set.contains(s)) continue;
                    set.add(s);
                }
            System.out.println(u + " " + n + " " + set.size());
        }

    }
}