题目描述

给你一个列表 nums，里面每一个元素都是一个整数列表。请你依照下面各图的规则，按顺序返回 nums 中对角线上的整数。

样例

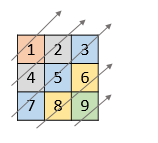
输入：nums = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,4,2,7,5,3,8,6,9]

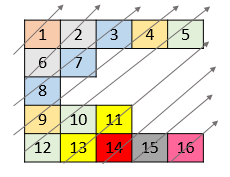
输入：nums = [[1,2,3,4,5],[6,7],[8],[9,10,11],[12,13,14,15,16]]
输出：[1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16]

输入：nums = [[1,2,3],[4],[5,6,7],[8],[9,10,11]]
输出：[1,4,2,5,3,8,6,9,7,10,11]

输入：nums = [[1,2,3,4,5,6]]
输出：[1,2,3,4,5,6]

限制

• 1 <= nums.length <= 10^5
• 1 <= nums[i].length <= 10^5
• 1 <= nums[i][j] <= 10^9
• nums 中最多有 10^5 个数字。

算法

(链表) $O(S)$

1. 枚举对角线，即横纵坐标的和 d。
2. 将当前所有行构建成一个双向链表，头结点初始化为 0。
3. 按对角线枚举，每次从链表的头开始，到第 d 行或者链表末尾结束，遍历其中的数字。
4. 如果发现当前的元素是这一行的最后一个元素，则我们将这一行从双向链表中删除。
5. 如果链表为空，则停止遍历。

时间复杂度

• 每个位置仅遍历一次，故时间复杂度为 $O(S)$，其中 $S$ 为数字的个数。

空间复杂度

• 需要额外 $O(n)$ 的空间维护双向链表，以及存储答案。

C++ 代码

class Solution {
public:
    vector<int> findDiagonalOrder(vector<vector<int>>& nums) {
        int n = nums.size();

        vector<int> pre(n + 1), nxt(n + 1);

        int s = 0;
        for (int i = 0; i <= n; i++) {
            pre[i] = i - 1;
            nxt[i] = i + 1;
        }

        int d = 0;
        vector<int> ans;

        while (s < n) {
            vector<int> cur;
            for (int i = s; i < min(d + 1, n); i = nxt[i]) {
                if (d - i < nums[i].size()) {
                    cur.push_back(nums[i][d - i]);
                    if (d - i == nums[i].size() - 1) {
                        if (pre[i] == -1) s = nxt[i];
                        else nxt[pre[i]] = nxt[i];

                        pre[nxt[i]] = pre[i];
                    }
                }
            }

            ans.insert(ans.end(), cur.rbegin(), cur.rend());
            d++;
        }

        return ans;
    }
};