题目描述

Given a list of lists of integers, nums, return all elements of nums in diagonal order as shown in the below images.

样例

Example 1:

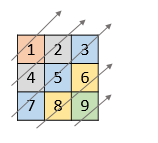
Input: nums = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,4,2,7,5,3,8,6,9]

Example 2:

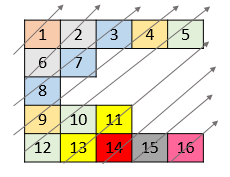
Input: nums = [[1,2,3,4,5],[6,7],[8],[9,10,11],[12,13,14,15,16]]
Output: [1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16]

Example 3:

Input: nums = [[1,2,3],[4],[5,6,7],[8],[9,10,11]]
Output: [1,4,2,5,3,8,6,9,7,10,11]

Example 4:

Input: nums = [[1,2,3,4,5,6]]
Output: [1,2,3,4,5,6]

Constraints:

• 1 <= nums.length <= 10^5
• 1 <= nums[i].length <= 10^5
• 1 <= nums[i][j] <= 10^9
• There at most 10^5 elements in nums.

算法

一看到对角线，我的第一反应是八皇后问题。在八皇后问题里，判断是否在同一主对角线还是同一次对角线时，主对角线上满足行号 - 列号差值相同，次对角线上满足行号 + 列号总和相同。

本题仅仅涉及次对角线，所以在同一对角线上的元素，必然满足i+j的值相同，其中i是行号，j是列号。那么只需要用一个unordered_map统计i+j对应的元素有哪些，注意点是输出的顺序是从左下到右上，那么就需要每个数组逆序输出。如果题目变化一下，从右上到左下输出，就每个数组正序输出即可，灵活掌握。

数组里的每个元素遍历两遍，设元素总数是$N$，时间复杂度$O(N)$

C++ 代码

class Solution {
public:
    vector<int> findDiagonalOrder(vector<vector<int>>& nums) {
        std::ios_base::sync_with_stdio(false);
        cin.tie(NULL);
        cout.tie(NULL);

        int n = nums.size();
        unordered_map<int, vector<int>> um;
        int maxSum = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < nums[i].size(); ++j) {
                um[i + j].push_back(nums[i][j]);
                maxSum = max(maxSum, i + j);
            }
        }

        vector<int> res;
        for (int i = 0; i <= maxSum; ++i) {
            for (int j = (int)um[i].size() - 1; j >= 0; --j) {
                res.push_back(um[i][j]);
            }
        }

        return res;
    }   
};